Системы автоматической стабилизации того или иного технологического параметра. Системы автоматического регулирования с запаздыванием, страница 19

Для скорректированной САР скорости двигателя постоянного тока , которой имеет вид рис.З2,б, можно ограничиться двумя трапециями (рис. 33,6),

Каждая трапеция характеризуется интервалом пропускания частот , высотой  и коэффициентом наклона  при определении численных значений которых следует две стороны трапеции совместить с осями координат.

3.   Произвести построение переходного процесса для каждой трапеции в отдельности при помощи таблиц - функций, которые построены для единичной трапеции (=1, =1, ).

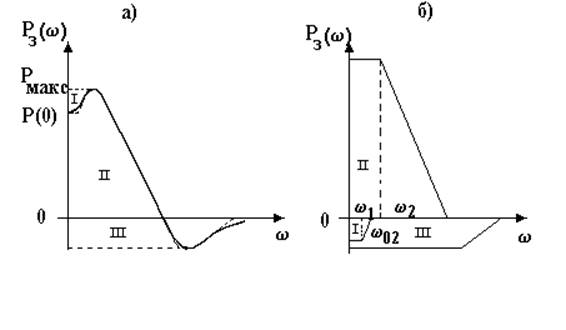
Рис. 32. Реальная вещественная частотная характеристика  (а) и ее аппроксимация трапециями (б).

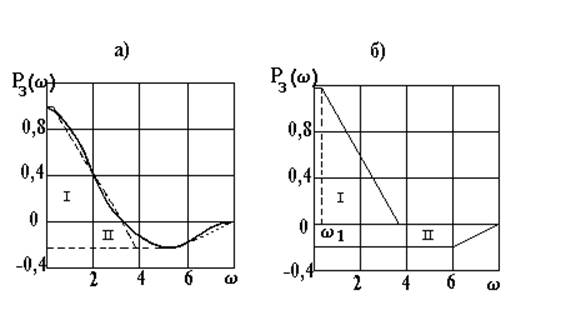
Рис. 33. Реальная Р(w) системы стабилизации скорости измельчительного агрегата - (а) и ее аппроксимация трапециями - (б).

Переход от - функций к переходным процессам, соответствующим характеристикам   и  , отличным от единицы, производится путем пересчета масштабов. Следует обратить внимание на то, что установившееся значение каждой переходной характеристики должно быть равно высоте соответствующей трапеции.

Суммирование этих переходных функций, соответствующих трапециям, определит переходной процесс в целом, анализируя который можно найти показателя качества.

На рис. 34 приведены кривые переходных процессов для САР скорости постоянного тока.

Если в соответствии с заданием на систему действует помеха, то следует проверить, не превосходит ли допустимого значения дисперсия флюктуационной составляющей ошибки.

Дисперсия ошибки _, обусловленная стационарным случайным воздействием, может быть получена интегрированием спектральной плотности ошибки :

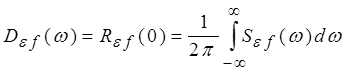, где  определяется исходя из известной спектральной плотности шума  и передаточной функции замкнутой скорректированной системы:

.

Определение  сводится при этом к вычислению интегралов:

.

Значения интегралов определяются по соответствующим таблицам в зависимости от порядка характеристического уравнения системы.

В соответствии с заданием необходимо построить область устойчивых состояний САР в плоскости двух параметров. Область устойчивости в таком случае представляет собой часть плоскости, ограниченную линиями - границами области устойчивости.

Условия нахождения системы на границах устойчивости могут быть выражены аналитическими зависимостями.

Нетрудно видеть, что один из вещественных корней характеристического уравнения

.

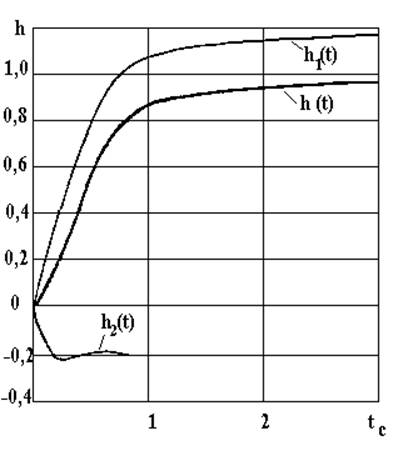
Рис. 34. График переходного процесса  в САР с корректирующим устройством при действии ступенчатого управления обратится в нуль тогда, когда коэффициент. Про такую систему говорят, что она находится на границе апериодической устойчивости (граница первого типа).

Равенство одного из корней характеристического уравнения минус бесконечности  соответствует границе третьего типа. Это возможно только при обращении в нуль коэффициента , что равносильно понижению степени характеристического уравнения на единицу.

Граница устойчивости второго типа - колебательной границе устойчивости - можно поставить в соответствие то или иное аналитическое выражение в зависимости от применяемого критерия устойчивости.

Так, например, границе колебательной устойчивости соответствует равенство нулю определителя Гурвица или прохождение кривой Михайлова через начало координат, т.е. если

, то

 и , и т.д.

Любое из этих условий можно использовать для нахождения границы устойчивости второго типа. И если будут найдены все три границы устойчивости, то тем самым будет найдена и область устойчивости, ограниченная ими. Область устойчивости принято обозначать штриховкой ее границ так, чтобы штрихи были направлены внутрь области устойчивости (рис. 35).

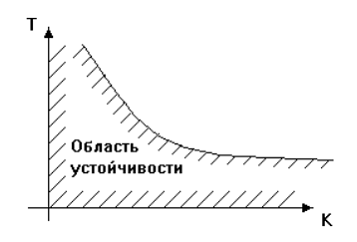
Рис. 35. К построению области устойчивости в плоскости двух параметров

В некоторых случаях сразу бывает затруднительно определить, какая из частей плоскости является областью устойчивости. В таких сомнительных случаях можно задаться любой точкой плоскости и при значениях  и , соответствующих этой точке,  проверить любым из критериев устойчивости системы. Если этой точке соответствует устойчивость, то и вся область, в которой находится рассматриваемая точка, является областью устойчивости.