Системы автоматической стабилизации того или иного технологического параметра. Системы автоматического регулирования с запаздыванием, страница 22

Очевидно, режим больших рассогласований соответствует насыщению электронного усилителя системы. Модель САР, соответствующая такому режиму работы,примет вид, изображенный на рис. 42.

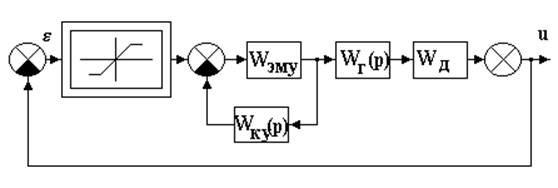
Рис. 42. Структурная схема CАP скорости в режиме больших рассогласований.

Среди известных методов исследования наиболее рациональным является метод; гармонической линеаризации, поскольку линейная часть исходной системы выше второго порядка и точные методы применить затруднительно.

Проверим применимость идеи гармонической линеаризации для рассматриваемой системы. Для этого необходимо, чтобы линейная часть системы удовлетворяла свойствам фильтра низких частот, т.е. чтобы линейная часть подавляла составляющие высших гармоник и пропускала лишь первую гармонику.

Определение параметров автоколебаний при использовании гармонической линеаризации основано на следующих соображениях. Если в реальной системе возможны автоколебания, то в близкой к ней линеаризованной системе должны также существовать колебания с постоянной амплитудой. Так как последняя линейна, колебания с постоянной амплитудой могут быть лишь в случае, если она находится на границе устойчивости, и, используя любое из математических условий нахождения системы на границе устойчивости, можно получить уравнения, связывающие параметры автоколебаний с параметрами системы. Если при всех возможных для данной нелинейности  система устойчива, то в ней не могут существовать автоколебания. Анализируя все известные методы, отметим, что для исследования данной системы значительное упрощение расчетов может быть достигнуто, если использовать логарифмические амплитудно-частотные и фазочастотные характеристики [6].

Методика расчетов сводится к следующему. Условие возникновения периодического режима в нелинейной системе в соответствии c критерием Найквиста может быть записано в виде [1 - 3,6].

или

;

.

Прологарифмировав это выражение, получим

, где

;

.

С учетом однозначности характеристики нелинейного звена условие возникновения колебаний примет вид

, где

, ;

; .

Коэффициент гармонической линеаризации для  нелинейности типа насыщения имеет вид

   ;

, ;

Для того чтобы логарифмические характеристики нелинейного звена стали универсальными и пригодными для исследования влияния параметров  и  на устойчивость и параметры автоколебаний, рационально  отнести к линейной части и ввести относительную амплитуду

.

Тогда, введя обозначение , получим следующие выражения для определения приведенных характеристик нелинейной части:

    при ;

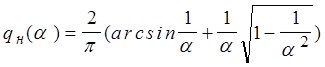     при      .

При       можно считать ,

.

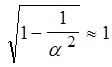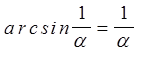Тогда                    .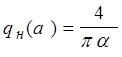

Логарифмируя, получаем

.

Зависимость  имеет вид, приведенный на рис. 43.

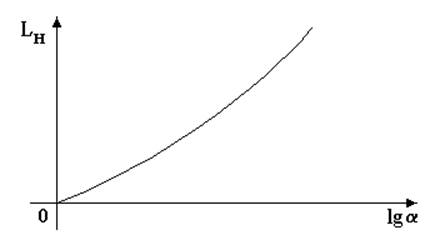
Рис. 43. Зависимость  от  для нелинейностей типа насыщения

Для определения условия автоколебаний строим в одних осях характеристики ,  и  (рис. 44).

Исследование влияния коэффициента усиления линейной части системы показывает, что при увеличении коэффициента передачи САР до некоторой величины вместо неустойчивости, которая следует из линейной теоремы, в системе возникают автоколебания (рис.44).

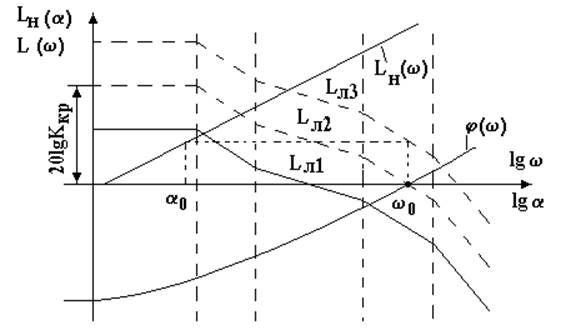
Рис.44. Условия возникновения автоколебаний в системе

Зависимости параметров автоколебаний от коэффициента передачи системы (рис.45) показывают, что при определении значений параметров возможна работа системы как в устойчивом режиме без автоколебаний, так и в автоколебательном установившемся режиме.

Рис.45. Графики изменения амплитуды и частоты автоколебаний от коэффициента передачи системы

В записку на этом этапе исследований необходимо включить:

составление модели САР в режиме больших рассогласований;

обоснование метода исследования свободного движения САР;

расчет коэффициентов гармонической линеаризации;

графики изменения параметров автоколебаний от одного из параметров системы.

При исследовании вынужденного движения системы с нелинейностями более сложного вида и более высоким порядком линейной части целесообразно использовать моделирование на ЭВМ.