Системы автоматической стабилизации того или иного технологического параметра. Системы автоматического регулирования с запаздыванием, страница 15

Второй случай:      (рис. 21).

Рис. 21. Логарифмические частотные характеристики  и  для случая

В том случае, если система маломощная, возможно применение последовательно включенных одинарных и двойных интегродифференцирующих и смешанных интегрирующих и интегродифференцирущих цепочек. Однако следует заметить, что если система имеет большое число инерционных элементов, то частота среза системы, скорректированной с помощью одинарной интегродифференцирующей цепочки, может быть расположена только левее сопрягающей частоты второй по величине постоянной времени исходной системы .

При применении двойных интегродифференцирующих устройств удается обеспечить большие запасы устойчивости по фазе, но при этом система становится чувствительной к высокочастотным помехам в сигнале на входе корректирующего устройства, т.е. практически всегда возникает необходимость в фильтрации помех.

Возможно также применение глубоких отрицательных обратных связей дифференцирующего характера.

В случае, если , в простых системах малой мощности предпочтительнее применение последовательных корректирующих устройств.

В системах же средней и большой мощности целесообразно использовать коррекцию в обратной связи или применять сложные корректирующие устройства.

Третий случай:        (рис. 22).

Рис. 22. Логарифмические частотные характеристики  и  для случая

В этом случае предпочтительным решением задачи является также последовательное включение двойных интегродифференцирующих цепочек или интегродифференцирующей-дифференцирующей цепочки. При этом желательно добиться уменьшения третьей по ве-личине постоянной времени исходной системы. При числе основных постоянных времени более трех коррекция существенно затруднена.

Применение же глубоких отрицательных обратных связей практически затруднено, так как в области частот левее , корректирующая обратная связь, хотя и может быть отрицательной, но окажется слабой. В области правее  она должна быть положительной, так как усиление скорректированной системы в этой области частот не меньше, а больше усиления нескорректированной системы.

Применение глубокой корректирующей обратной связи возможно только при условии значительного завышения коэффициента передачи исходной системы по сравнении с желаемым коэффициентом передачи.

Четвертый случай:                 (рис. 23).

В этом случае основным способом коррекции является последовательное включение в прямую цепь одинарных и двойных дифференцирующих цепочек. Причем необходима, как правило, фильтрация высокочастотных помех. При числе основных постоянных времени более трех коррекция практически невозможна.

Рис. 23. Логарифмические частотные характеристики  и  для случая

При таком соотношении частот среза применение глубокой отрицательной обратной связи невозможно, так как  либо совпадает с  (область низких частот), либо проходит выше (область средних и высоких частот).

В ряде случаев возможно применение положительной корректирующей связи, методика расчета которой остается прежней. При этом необходимо проверить динамические свойства системы при отклонениях параметров, вызываемых изменением внешних условий.

Анализ возможных случаев соотношения частот среза ЛАХ желаемый нескорректированной систем приводит к выводу, что прежде чем вводить корректирующее устройство в прямую или обратную связь, целесообразно исследовать возможность уменьшения постоянных времени функциональных элементов системы. Это достигается выбором менее инерционных функциональных элементов, что позволяет существенно упростить вид корректирующего устройства и тем самым уменьшите его чувствительность к помехам, неучтенным нелинейностям и изменению параметров системы.

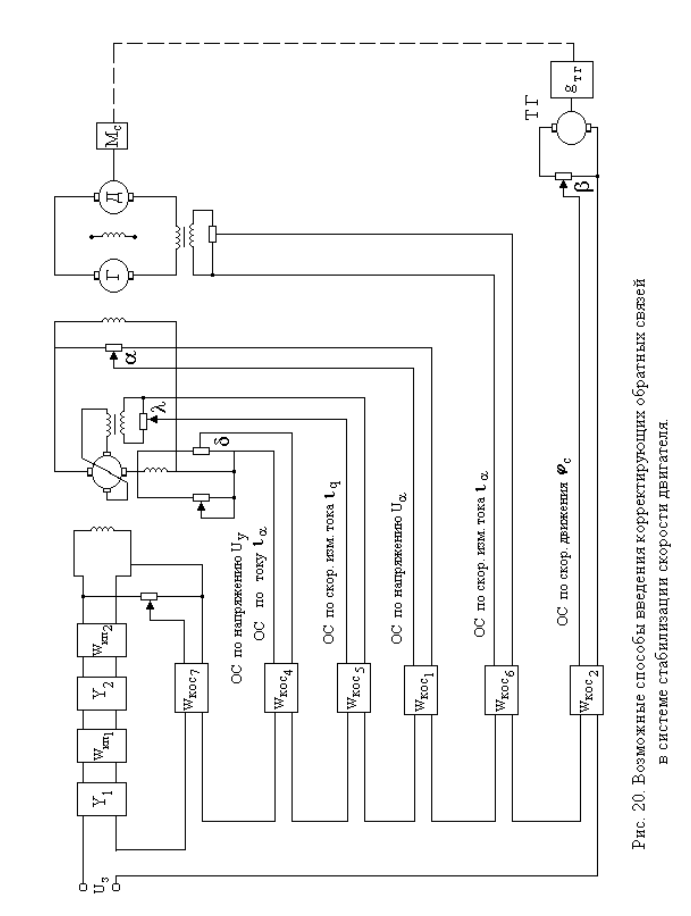
Рассмотрим пример синтеза корректирующего устройства для системы стабилизации скорости приведения мельничного агрегата. Исходя из выбранного еще на этапе анализа частотного метода, учитывая, что система статическая и на нее не действуют помехи, выберем метод синтеза по ЛЧХ- метод Солодовникова.