Системы автоматической стабилизации того или иного технологического параметра. Системы автоматического регулирования с запаздыванием, страница 8

Итак, в рассматриваемом примере за основную принимается линейная модель. Описание функциональных элементов системы широко приводится в литературе [1-4.], а также проводилось в рамках курсовой работы по курсу "Теоретические основы кибернетики" и принципиалъных трудностей не должно вызывать. В данной работе передаточные функции записываются без вывода, указывается лишь ссылка на источник, откуда они взяты.

Структурная схема системы стабилизации скорости привода мельничного агрегата примет вид рис. 5.

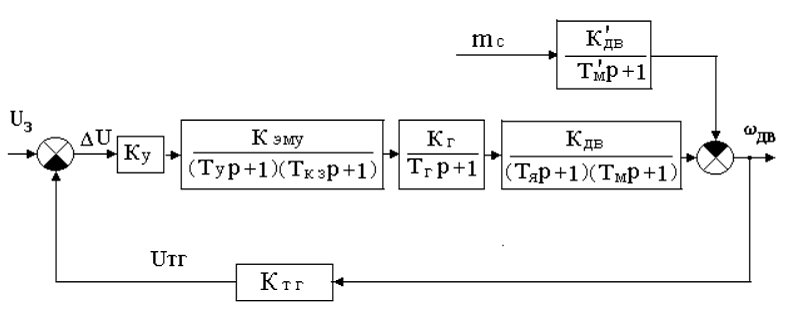Рис. 5. Структурная схема САР скорости вращения мельничного агрегата

Следует обратить внимание на численные значения постоянных времени функциональных элементов, приводимых в исходных данных, и, если есть постоянные, существенно отличающиеся друг от друга (более чем на два порядка), можно понизить порядок такой системы без потери ее динамических свойств.

Так, в данном примере такими постоянными являются  электромашинного усилителя и  двигателя. Структурная схема может быть упрощена до вида рис. 6.

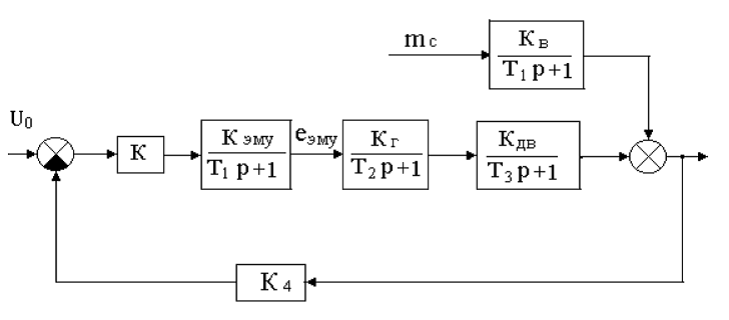
Рис. 6. Упрощенная структурная схема САР скорости вращения мельничного агрегата

В заключение этого этапа (если это необходимо) целесообразно привести структурную схему системы к схеме с единичной обратной связью, так как методы, применяемые в инженерных расчетах, рассчитаны на системы с единичной отрицательной связью, что позволяет придать этим методам некоторую общность применения для целого класса. Такое преобразование не вызывает трудностей, так как обратная связь жесткая, и перенесение звена в обратной связи в прямую цепь соответствует лишь некоторому масштабированию, так как выходной величиной теперь является измеряемая с помощью датчика истинная выходная переменная системы.

В примере с САР скорости вращения мельницы после переноса тахогенератора в прямую цепь выходной переменной системы является уже напряжение тахогенератора _.

Структурная схема примет вид рис. 7.

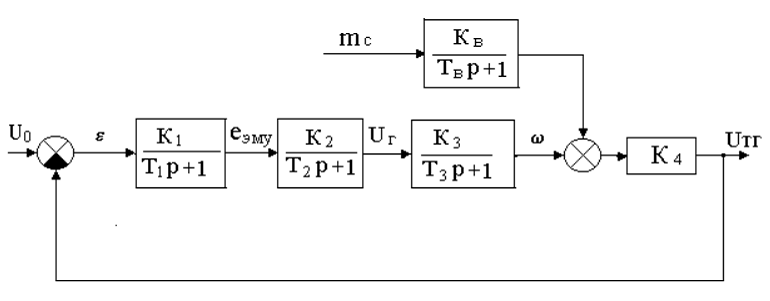
Рис. 7. Преобразованная структурная схема САР скорости вращения мельничного агрегата

В результате формализации задачи в пояснительной записке на основе содержательного анализа исходной схемы должна быть приведена аргументированная классификация системы, обоснованный выбор типа математической модели, описание ее функциональных элементов и, если это возможно, ее упрощение.

5.2. Анализ исходной САУ

На этом этапе выполнения курсовой работы важно прежде всего выбрать метод расчета системы, т.е. метод, который позволил бы решить с достаточной простотой и задачу анализа и задачу синтез, исходными данными для ответа на этот вопрос являются вид модели, соотношение ее постоянных времени, требования к динамическим свойствам системы. Так, в рассматриваемом примере методы анализа следует искать среди методов классической теории управления, которые основаны на преобразованиях в плоскости комплексного переменного, т.е. частотных и корневых методов расчета. Заметим, что в практике расчета широкое распространение получили инженерные методы, основанные на использовании логарифмических частотных характеристик [1-3, 5- 8], так как эти методы позволяют в процессе синтеза корректирующего устройства определить как его структуру, так и параметры. Кроме того, эти методы снабжены большим количеством удобных номограмм, графиков, зависимостей, позволяющих быстро производить приближенный анализ и синтез линейных САУ.

Если требуется выбрать метод исследования устойчивости и оценки качества в переходном и установившемся режиме, то следует выбирать такой, который позволит с меньшими вычислительными затратами оценить и устойчивость и качество.

Пусть требуется провести анализ исходной системы и в качестве метода анализа и синтеза выберем частотный, основанный на построении логарифмических частотных характеристик (ЛЧХ). Естественно при этом определять устойчивость системы и ее запасы по ЛЧХ [5]. Поскольку система минимально-фазовая с устойчивой разомкнутой частью, то оценка устойчивости не вызывает трудностей (рис. 8). Запасы по модулю составляют =5 дБ, а по фазе - 22,5°.