Введение. Предмет, цель и содержание курса. Взаимосвязь методов системного анализа ИС. Моделирование экономических и информационных процессов системами и сетями массового обслуживания, страница 7

Дисперсия является суммой двух слагаемых, первое из которых равно взвешенной сумме (с коэффициентами -  средним числом посещений узла Mn_j ) дисперсий времени пребывания заявки в каждой  СМО, второе – взвешенной сумме (с коэффициентами  cov (n_j n_m)) попарных произведений средних времён пребывания заявки в каждой СМО сети. Для ряда частных структур сетей – последовательной, параллельной, циклической  из общей формулы получены простые выражения для расчёта Dt_q . В последовательной СеМО имеется М последовательно соединённых СМО. Заявки поступают в первую систему, из неё во вторую и так далее. После обслуживания в системе М заявки покидают сеть. Решения для T_q и Dt_q имеют вид:

M                                  M

T_q = åT_qi  ,                  Dt_q = åDt_qi                                                    i=1                                 i=1

В параллельной СеМО  со случайным ветвлением заявок входящие заявки попадают с вероятностью р_j в   j – ю СМО и после обслуживания покидают сеть. Решения для T_q и Dt_q имеют вид:

M                                                  M

T_q = å  p_i T_qi     ,                         Dt_q = å  p_i (Dt_qi + T_qi² ) -     T_q²              i=1                                                i=1

В циклической СеМО  заяявки поступают в первую СеМО, а из неё с вероятностью р во вторую СеМО ( или с вероятностью 1-р покидают сеть), из второй СМО снова в первую и так далее. Решения для T_q и Dt_q имеют вид:

1                  p

T_q = ¾¾ Т_q1 +    ¾¾  Т_q2

(1-р)             (1-p)

1                 p                      p

Dt_q = ¾¾ Dt_q1 + ¾¾  Dt_q2  + ¾¾    (T_q1  +  T_q2 )²

(1-р)             (1-p)               (1-p)²

Выделяя в любой открытой СеМО последовательные, параллельные и циклические структуры  (подсети) можно вычислить показатели производительности по приведённым формулам. Предоставляем читателю найти дисперсию времени задержки  Dt_q для примера, приведённого на рис.4.8.

Рассмотрим пример расчёта показателей производительности  замкнутой однородной экспоненциальной СеМО с узлами М/M/1/¥, которая моделирует диалоговые системы обработки. Такая система допускает подключение ограниченного числа М рабочих станций к серверу, каждая из которых работает в режиме диалога.  В этом режиме новая заявка от рабочей станции не генерируется к серверу до тех пор, пока не будет получен ответ на предшествующую заявку.  Функциональная модель диалоговой системы представлена на рис. 8.5. В ней можно выделить терминальную подсистему и  подсистему передачи и обработки. Терминальная подсистема  содержит  М узлов, которые моделируют действия пользователей за рабочей станцией. В простейшем случае это подготовка сообщения для передачи и ожидание ответа на переданное сообщение. Предполагается, что каждый узел i  терминальной подсистемы представляет собой СМО М/M/1/¥ с дисциплиной обслуживания очереди FCFS. Очереди к приборам в терминальной подсистеме отсутствуют, поскольку в случае  диалогового режима число заявок во всей сети равно числу терминалов. Подсистема передачи и обработки содержит N узлов, которые моделируют процесс передачи сообщения (ЛВС, “последняя миля”, транспортная сеть) и его обработки сервером. Сохраним предположение о экспоненциальности функции распределения вероятностей времени обслуживания в узлах с параметром m_i  i=1,2,..N. Маршрутизация заявок в сети по- прежнему будет определяться вероятностями перехода p_ij i,j=0,1,2,..N, где под источником заявок будем понимать терминальную подсистему (система S₀). При этом, учиN

тывая, что заявки не покидают сеть, имеем å  p_ij =1, i=0,1,2,..M. Также предполагается,                                                                             j=0 что маршрутная стохастическая матрица Р=(р_ij)    i,j=0,1,2,..M  является неразложимой.

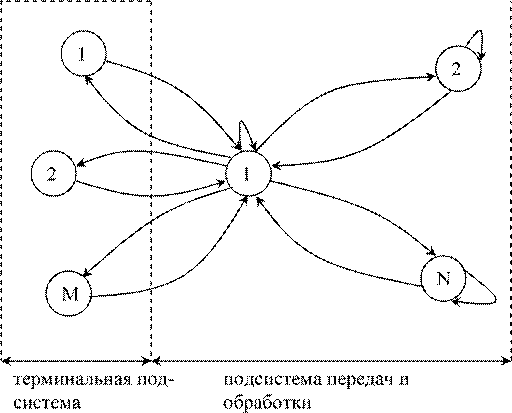
Рис.8.5. Функциональная модель диалоговой системы

Таким образом, для сети задано описание:

терминальной подсистемы

1.  число узлов (диалоговых пользователей рабочих станций) – М;