13. Стационарное среднее значение времени ожидания начала обслуживания. Находится по определению математического ожидания непрерывной случайной величины:
¥ 1 r
Tw = ò t d Ftw(t) = ¾ ¾
0 m (1-r)
Аналогичный результат можно получить по формуле Литтла Tw = Lw/l.
14. Функция распределения вероятностей времени пребывания в системе Ftq(t). Находится по формуле:
Ftq(t) = 1 – exp(-m(1-r)t), t>0.
Смысл формулы состоит в том, что заявка проводит в системе М/М/1/¥ случайное время, распределённое по экспоненциальному закону с параметром m(1-r).
15. Стационарное среднее значение времени пребывания в системе. Находится по определению математического ожидания непрерывной случайной величины:
¥ 1 1
Tq = ò t d Ftq(t) = ¾ ¾
0 m (1-r)
Аналогичный результат можно получить как по формуле Литтла Tq = Lq/l., так и сложив среднее время в очереди и приборе Tq = M(tw(w) + tk(w))= Tw+Ts.
16. Стационарное значение дисперсии времени пребывания в системе. Находится по определению дисперсии непрерывной случайной величины в предположении независимости ожидания и обслуживания:
Dtq = D(tw(w) + tk(w))= Dtw+Dts = Dtw+ 1/m2 Первое слагаемое будет равно:
¥ 1 (2 - r)r
Dtw = ò (t – T w )2d Ftw(t) = ¾¾ ¾¾¾¾
0 m2 (1 - r )2
Окончательно получим выражение для вычисления дисперсии времени пребывания в системе:
1 (2 - r)r 1
Dtq = ¾¾ ¾¾¾¾ + ¾¾
m2 (1 - r)2 m2
17. Выходящий поток из функционирующей в стационарном режиме системы М/М/1/¥ является пуассоновским интенсивности l.
Полученные результаты позволяют спроектировать систему массового обслуживания например таким образом, чтобы время пребывания заявки в системе не превышало допустимую величину tдоп (пусть 0.5с.) для заданой части входящих заявок (пусть 90%). Если задать загрузку системы на уровне 0.7, то значение m может быть найдено из нелиненйного уравнения: 1 – exp(-m(1-0.7)0.5) = 0.9, m>0. Значение интенсивности входного потока находится из условия l=0.7m. Затем по найденным l, m вычисляются все показатели производительности системы 1- 17.
Разработка функциональных моделей технических устройств на достаточно глубоком уровне детализаации требует их представления в виде сетей массового обслуживания. Сетью массового обслуживания называется взаимосвязанная совокупность конечного числа систем массового обслуживания (узлов). Узлом сети массового обслуживания является система массового обслуживания некоторого типа, например М/М/N/r. Для описания узла СеМО должно быть дано:
-среднее время обслуживания заявки в приборе1/m
-дисциплина обслуживания заявок;
-параметры СМО узла N, r; Ограничения:
-приборы не простаивают, когда в узле есть заявки;
-заявки не могут покидать узел недообслуженными;
-объем незавершенной работы в приборе не зависит от дисциплины обслуживания; -заявка не может одновременно обслуживаться (или ожидать) в двух или более узлах; -каждая заявка обслуживается отдельным прибором.
Узел, объединяющий все потоки заявок, поступающие в сеть, называется источником заявок. Узел, объединяющий все выходящие из сети заявки, называется стоком заявок. Различают открытые, замкнутые и смешанные сети массового обслуживания. СеМо называется разомкнутой (открытой), если в ней существуют источник заявок и сток заявок, и интенсивность источника заявокLне зависит от состояния сети (т.е. от числа заявок, поступивших в сеть) (рис 8.1.).
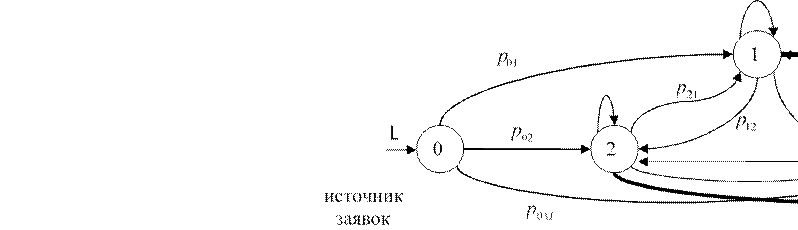
Рис. 8.1. Открытая сеть массового обслуживания
СеМО называется замкнутой, если в ней нет источников заявок и стоков заявок, интенсивность источника зависит от состояния сети и число циркулирующих одних и тех же заявок всегда постоянно и равно М (рис.8.2.).

Рис. 8.2. Замкнутая сеть массового обслуживания
СеМО называется смешанной, если для одной части узлов и потоков заявок она является открытой, для другой части – замкнутой.

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.