Введение. Предмет, цель и содержание курса. Взаимосвязь методов системного анализа ИС. Моделирование экономических и информационных процессов системами и сетями массового обслуживания, страница 17

Найдем время распространения сигнала при следующих данных: расстояние между отправителем и получателем 800 км.

T_рас = 800 /90000 = 0,008 с.

Определим задержку приемной ЛВС при следующих данных:

Длина пакета E_п = 1024 байт или 8192 бит.

Vш = 100 Мбит/с.

Длина шины Sш = 300 м.

Скорость распространения сигнала на шине Vc = 90000 км/c

T_ЛВСпрм  = 8192/1000000 + 0,3/90000 = 0,18 с.

Тогда доставка сообщения Tд = 0,0000874 + 0,008 + 0,37 + 0,0035 + 0,18 = 0,55 с.

3. Оптимизация экономических  и информационных систем (4 часа)

1. Задача определения оптимальной производительности серверов информационно - вычислительной сети

Рассмотрим схему технических средств КИС, приведенную  на рис. 2.1.1.  Одной из главных задач является выбор оборудования для центрально вычислительного комплекса (ЦВК). Центральный вычислительный комплекс обеспечивает хранение и обработку корпоративных данных. Доступ конечных пользователей к прикладным процессам обработки, функционирующим на серверах ЦВК, а через них к корпоративным данным, решается с помощью сети доступа. При объединении ПЭВМ и серверов  с помощью средств передачи данных  клиенты получили возможность работать со многими приложениями на специализированных серверах. Данные распределяются  между серверами в зависимости от потребностей прикладных задач,

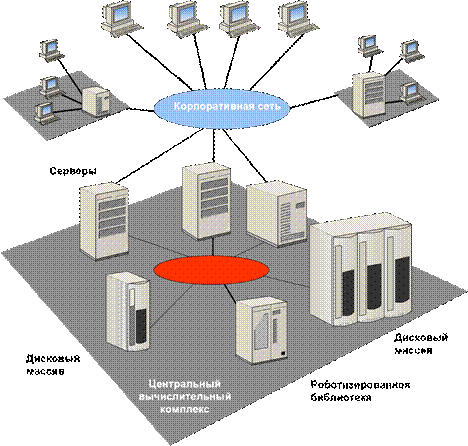
Рис. 2.1.1. Схема ЦВК регионального оператора связи

 Состав, типы и мощности серверов определяются индивидуально для каждого регионального оператора связи, интенсивности запросов и перечня оказываемых услуг, а также с учётом перспектив развития.

Рассмотрим простейшую структурную модель ЦВК в виде параллельно функционирующих несвязанных серверов (рис. 2.1.2.)

Рис. 2.1.2.  Структурная модель ЦВК.

Поступающая в ЦВК нагрузка распределяется диспетчером между серверами в соответствии с вероятностями P₁…. Р_N. Оптимальное обслуживание входящей нагрузки связано с согласованием производительности каждого сервера  с заданной диспетчером для этого сервера нагрузкой при условии, что средняя задержка любого сообщения в сети будет минимальной.

В качестве функциональной модели ЦВК примем открытую параллельную сеть массового обслуживания со случайным ветвлением заявок. Каждый сервер будем моделировать одноканальной системой массового обслуживания M/M/1. Предполагается что известен входной поток заявок в сеть и вероятности передач (распределение) заявок по системам (рис. 2.1.3).

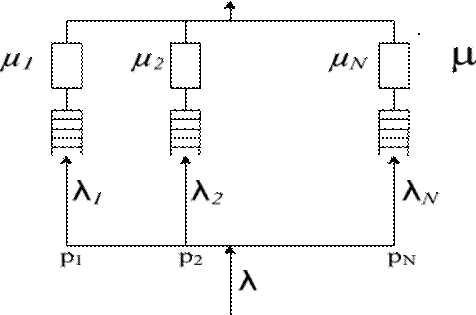
Рис. 2.1.3 Функциональная модель ЦВК сети.

Постановка задачи оптимизации производительности серверов  ЦВК.

Дано:

N – изолированных серверов и их модели в виде систем М/М/1 l  - общий входной поток заявок в сеть

^m  - общая производительность ЦВК ^pi - вероятности распределения заявок по серверам, i = 1, 2…N,  так что ^{li = pil}

Найти: такие производительности серверов  ЦВК μ₁…..μ_N, при которых средняя задержка  любого задания в сети будет минимальной:

^{N                                                             N l}

Tq (m1...mN ) = min{mi åi=1 p_iT_qi (m_i /l_i ) = min{mi } åi=1 _lⁱ _mi ¹_-li                                                                                                                                            (2.1)

}

Ограничения:

N

åm_i =m

ⁱ⁼¹                                                                                                                                                                                                              (2.2)

^mi  >li ³ 0 i=1,2,…N

Решение:

Рассмотрим критериальную функцию (2.1). Критериальная функция  является аддитивной функцией величин Tq_i, каждая из которых есть выпуклая функция μ_i. Тогда критериальная функция (2.1) также будет выпукла.Докажем это. Найдём частные производные

 =                           

i                            i è

     ìí^ïïïﶶ¶¶Tmm2Tqiiq2i =lllli i¶-m¶ 2æçç((mmmiii -1--llliii))ö÷÷ø×2(=-l1l)i =(m2ill--i1l× i()m2i <-1l0 i )2 > 0i = 1,2,..N                          (2.3)

î