Учбово-методичний посібник для виконання лабораторних робіт з дисципліни „Основи теорії криптографії і криптоаналізу”, страница 50

В нашій роботі спробуємо апроксимувати псевдовипадкову послідовність кубічним поліномом вигляду f(i) = a + bі + cі² + dі³, причому і знаходиться в діапазоні 0..35 включно (таким чином тренд охоплює 36 чисел псевдовипадкової послідовності відповідно до 36 чисел шифровки). На практиці користуються значно складнішими залежностями, але там і ставки вище. Отже нам треба знайти чотири коефіцієнти a, b, c, d по перших 32 числах (від 0 до 31), а тоді підставивши замість і 32, 33, 34, 35 знайти останні 4 числа гами. Для визначення коефіцієнтів скористаємося методом найменших квадратів [5]. Він розглядає суму квадратів різниць значень тренду і самої псевдовипадкової послідовності:

,       (1)

де у_і – і-те значення псевдовипадкової послідовності (тобто у₀ = 136, у₁ = 88 і т.д., якщо взяти вищенаведений приклад). Причому тут функція f(i) (тобто сам тренд) не є відомою. Для того, щоб тренд був найбільш “схожим” на саму псевдовипадкову послідовність, метод найменших квадратів вимагає, щоб вказана сума була найменшою:

      (2)

З цієї умови визначимо f(i). Як відомо з курсу вищої математики, необхідною умовою екстремуму функції є рівність нулю похідних від усіх змінних. Якщо записати в розгорнутому вигляді вираз (1) для нашого випадку матимемо:

        (3)

З (3) бачимо, що Q – функція чотирьох змінних, адже вона залежить тільки від значень a, b, c, d (у_і – фіксовані наперед задані значення). Отже, умова рівності нулеві всіх похідних запишеться так:

   (4)

Умови (4) є наслідком (2), і їх можна записати в розгорнутому вигляді, диференціюючи (3) по відповідним змінним:

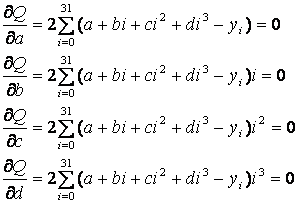      (5)

Перетворюючи (5) далі, маємо систему алгебраїчних рівнянь четвертого порядку:

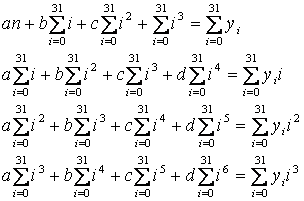     (6)

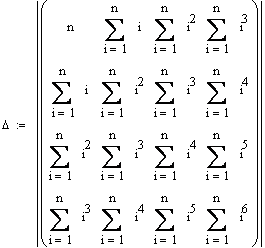
Таку систему можна вирішити одним із відомих методів, ми пропонуємо формули Крамера, як такі, де обчислення можна перекласти на комп‘ютер. Для цього обчислимо 5 визначників, наприклад в програмі MathCad:

де D – Головний визначник системи:

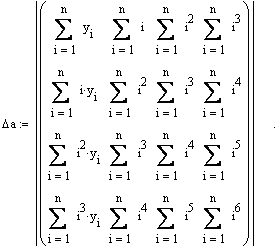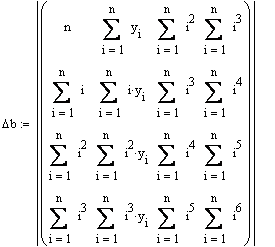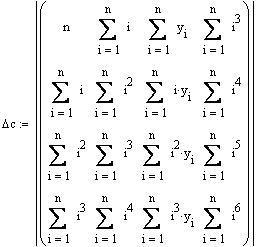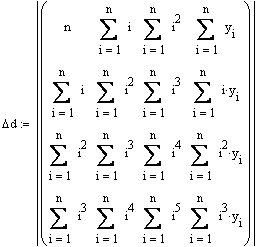Зауважимо, що наперед визначили n = 31, y_i визначаємо або поелементно (у₀ = 136, у₁ = 88, і т.д.), або створивши матрицю 32´1 і заповнивши відповідні місця. В знаках сум і змінюється від 1 до n, нульовий елемент не враховуємо, бо він все рівно дає нуль при будь-яких операціях над ним. Шукані коефіцієнти знаходимо як частки від ділень:

.

Коли знатимемо ці коефіцієнти, підставляємо у f(i) і = 32, 33, 34, 35. Отримаємо 4 числа в діапазоні 0..255. Накладаємо їх операцією XOR на відповідні останні чотири байти шифровки і маємо секретний код доступу.

Порядок виконання лабораторної роботи

1.  Вивчити математичні основи злому шифрів гамування.

2.  У завданні до лабораторної роботи (додаток 1) подані деякі псевдовипадкові послідовності.

3.  Необхідно за допомогою методу найменших квадратів якомога ближче аппроксимувати подану послідовність поліномом 3 ступеня.

4.  У звіті вказати отримані коефіцієнти поліному, а також обчислити його значення у заданих точках, занести ці значення до таблиці і навести відповіді на контрольні питання.

Контрольні питання

1.  Що таке потоковий шифр?

2.  У чому полягають основні переваги і недоліки потокових шифрів?

3.  Опишіть алгоритм апроксимації застосований у даній роботі?

4.  Яка основна умова можливості даного виду криптоаналізу?

5.  Як можна отримати фрагмент відкритого тексту для аналізу?

6.  Від чого залежить точність методу найменших квадратів?

Додатки

Додаток 1.  Вхідні дані до лабораторних робіт 1-17.

Лабораторна робота №1

Одиночна перестановка по ключу

1.  УЧБОВИЙ_ПОСІБНИК       (ГОРЩИК)

2.  ДЕТЕКТИВНА_ГРУПА      (ВОДА)

3.  ДЖЕРЕЛО_ЖИВЛЕННЯ    (ОБІД)

4.  ПУСКОВІ_ПРИСТРОЇ                  (ГРІМ)

5.  СИСТЕМА_ПЕРЕДАЧІ       (ОБІД)

6.  СИСТЕМА_ПРИЛАДІВ      (ВОДА)

7.  ЗНАЧЕННЯ_НАПРУГИ      (ГРІМ)

8.  ВИНОСНІ_ПРИСТРОЇ                 (ГОРЩИК)

9.  ОПОВІЩЕННЯ_ЛЮДЕЙ    (ОБІД)

10.  ПІДОХОРОННА_ЗОНА      (ВОДА)

11.  ЗБЕРЕЖЕННЯ_МАЙНА     (ГОРЩИК)

12.  УСТАНОВЛЕНІ_МЕЖІ       (ГРІМ)

13.  ТЕХНІЧНИЙ_ЗАХИСТ       (ГОРЩИК)

14.  СКЛАДОВІ_ЧАСТИНИ       (ГРІМ)

15.   КОМЕРЦІЙНІ_ФІРМИ       (ВОДА)

16.   НАЯВНІСТЬ_ЗАГРОЗ                 (ОБІД)

17.   КОМЕРЦІЙНИЙ_СОЮЗ    (ГОРЩИК)

18.   МІЛЬЯРДИ_ДОЛАРІВ        (ВОДА)

19.   ЗАКОРДОННІ_ФІРМИ       (ГРІМ)

20.   РОЗБІЙНІ_НАПАДИ          (ГРІМ)

21.   ГРОШОВІ_ПЕРЕКАЗИ      (ГОРЩИК)

22.   ГОТОВНІСТЬ_СЛУЖБ       (ВОДА)

23.   ПІДКУП_ПЕРСОНАЛУ      (ГРІМ)

24.   ФІЗИЧНА_РОЗПРАВА       (ГОРЩИК)

25.   НАЙБІЛЬШ_ВАЖЛИВІ      (ГРІМ)

26.   РОЗРОБКА_ЗАСОБІВ                 (ОБІД)

27.   ДІЇ_ЗЛОВМИСНИКІВ                 (ГРІМ)

28.   АНАЛІТИЧНА_ГРУПА      (ОБІД)

29.   СПРИЯТЛИВІ_УМОВИ     (ГОРЩИК)

30.   ТАЄМНОСТІ_РОБОТИ      (ОБІД)

Подвійна перестановка по ключу (зашифрувати)

№	Шифровка	КЛЮЧІ
1	ВАЖЛИВЕ_ЗНАЧЕННЯ	1973,1649
2	ПРИКЛАД_ЗАВДАННЯ	1578,4697
3	СМУГОВИЙ_ФІЛЬТР_	5486,4658
4	ОБРОБКА_КАПУСТИ_	1354,1589
5	ВАЖЛИВА_ВКАЗІВКА	1562,1543
6	РОЗШИРЕНА_МЕРЕЖА	1564,2165
7	АБСТРАКТНИЙ_ТИП_	3214,5461
8	РОЗУМНИЙ_СЛОВНИК	4589,6871
9	ЛІНІЙНА_АЛГЕБРА_	1579,1563
10	НАЙБІЛЬШ_ВАЖЛИВІ	5632,2145
11	НОРМАЛЬНА_ФОРМА_	7458,5896
12	РОСІЙСЬКИЙ_ТЕКСТ	1296,0456
13	АБСТРАКТНИЙ_КЛЮЧ	1235,1053
14	СОЛОДКЕ_МОРОЗИВО	5034,3698
15	ВЕЛИКЕ_ДЗЕРКАЛО_	1589,1493
16	ЗЧИТУВАННЯ_ШИФРУ	1579,1593
17	СТАРЕНЬКА_МАШИНА	5487,3698
18	ТАЄМНОСТІ_РОБОТИ	1789,9632
19	ДВІЙКОВА_СИСТЕМА	1354,5682
20	СТРУКТУРА_ДОМЕНУ	0673,1248
21	ХУТРЯНА_КУРТОЧКА	1257,1653
22	ЗА_ТРИСТА_РОКІВ_	1563,2647
23	КЛЮЧ_ШИФРУВАННЯ_	6578,3429
24	СТІЙКІСТЬ_ШИФРУ_	5863,5463
25	ПАЛІННЯ_ШКІДЛИВЕ	1576,4562
26	ПРИКЛАДИ_ТЕКСТІВ	2163,1684
27	ТРЕБА_ЇСТИ_КАШУ_	2613,1350
28	ОЦІНИТИ_ПОРЯДОК_	1534,4563
29	СПРАВА_РОЗКРИТА_	2583,3571
30	РОЗКРИТТЯ_ШИФРІВ	1596,3242