Але будь-яке квадратичне відрахування а задовольняє при деякому х порівнянню a ºx2 (mod p) і, отже, задовольняє також одержуваному з нього зведенням у ступінь (p – 1)/2 порівняння a(p -1)/2 ºxp-1 º1(mod p) (знову теорема Ферма). При цьому, квадратичними відрахуваннями і вичерпуються всі рішення порівняння a(p -1)/2 º1(mod p), тому що, будучи порівнянням ступеня (p – 1)/2, воно не може мати більш ніж (p – 1)/2 рішень. Це означає, що квадратичні невідрахування задовольняють порівнянню a(p -1)/2 º-1(mod p)
Перелічимо далі найпростіші властивості символу Лежандра.
Властивість 3.8.1. Якщо a ºb (mod p ), то L(a, p) = L(b, p). [11]
Ця властивість випливає з того, що числа одного класу по модулю р будуть всі одночасно квадратичними відрахуваннями або квадратичними невідрахуваннями.
Властивість 3.8.2. L(1, p)=1.
Доказ очевидний, адже одиниця є квадратом.
Властивість 3.8.3.
Доказ цієї властивості випливає з критерію Ейлера при а = -1. Через те що ( p – 1)/2 – парне, якщо р виду 4 n +1, і непарне, якщо р виду 4 n +3, то число -1 є квадратичним відрахуванням по модулю р тоді і тільки тоді, коли р виду 4 n +1.
Властивість 3.8.4. L(ab, p) = L(a, p)L(b, p) [11]
Дійсно,
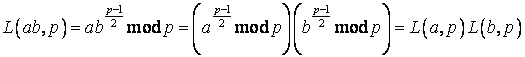
Властивість 3.8.4., поширюється на будь-яке кінцеве число співмножників у чисельнику символу Лежандра, взаємно простих з р. Крім того, з нього випливає
Властивість 3.8.5. 
, тобто в першому числі символу Лежандра
можна відкинути будь-який квадратний множник. [11] Дійсно:
, тому що незалежно від того чи буде 
або 
, 
.
Для визначення символу Лежандра можна скористатися наступним алгоритмом:
1. Якщо а = 1, то L(a, p) = 1
2.
Якщо а парне, то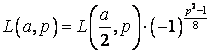 
3.
Якщо а непарне L(a, p), то 
Символ Якобі, J(a, n), являє собою узагальнення символу Лежандра на складені модулі, він визначається для будь-якого цілого a і будь-якого непарного цілого n. [1] Функція зручна при перевірці на простоту. Символ Якобі є функцією на множині отриманих відрахувань дільників n і може бути обчислений по різних формулах. Ось один із способів:
Визначення 3.9.1: J(a, n) визначений, тільки якщо n непарне.
Визначення 3.9.2: J(0, n) = 0.
Визначення 3.9.3: Якщо n – просте число, то символ Якобі J(a, n) = 0, якщо а поділяється на n.
Визначення 3.9.4: Якщо n – просте число, то символ Якобі J(a, n) = 1, якщо а – квадратичне відрахування по модулю n.
Визначення 3.9.5: Якщо n – просте число, то символ Якобі J(a, n) = -1, якщо а не є квадратичним відрахуванням по модулю n.
Визначення 3.9.6: Якщо n – складене число, то символ Якобі J(a, n) = J(a, p1)× ... × J(a, pm), де p1, ... , pm – це розкладання n на прості співмножники.
Наступний алгоритм рекурсивно розраховує символ Якобі:
Правило 3.9.1: J(1, n) = 1
Правило 3.9.2: J(ab, n) = J(a, n) J(b, n)
Правило 3.9.3: J(2, n) =, якщо (n2-1)/8 непарне, і -1 у противному випадку
Правило 3.9.4: J(a, n)= J((a mod n), n)
Правило 3.9.5: J(a, b1b2) = J(a, b1) J(a, b2)
Правило 3.9.6: Якщо найбільший загальний дільник a і b = 1, а також a і b непарні:
Правило 3.9.6а: J(a, b)= J(b, а), якщо (a – 1)(b – l)/4 парне
Правило 3.9.6b: J(a, b)= –J(b, а), якщо (a – 1)(b – 1)/4 непарне
Ось алгоритм мовою C++ [6]:
long Jacobi(long a,long p)
{
long g;
if(a>=p)a=a%p;
if(a==0)return 0;
if(a==1)return 1;
if(a<0)if((p-1)/2 % 2 == 0)return Jacobi(-a,p);
else return -Jacobi(-a,p);
if (a % 2 == 0)
if (((p*p -1)/8) % 2 == 0)
return +Jacobi(a/2,p);
else
return -Jacobi(a/2,p);
g = NOD(a,p);
if(g==a) return 0;
else if(g!=1)return Jacobi(g,p)*Jacobi(a/g,p);
else if(((a-1)*(p-1)/4)%2==0)return +Jacobi(p,a);
else return -Jacobi(p,a);
}
Якщо заздалегідь відомо, що n – просте число, замість використання попереднього алгоритму просто обчисліть a((n – 1)/2) mod n, у цьому випадку J(a, n) еквівалентний символу Лежандра L(a, n).
Символ Якобі не можна використовувати для визначення того, чи є а квадратичним відрахуванням по модулю. [1]
Визначення 3.10.1. Якщо p – просте число, і g менше, ніж p, то g називається генератором по модулю p, якщо для кожного числа b від 1 до p – 1 існує деяке число a, що ga º b (mod p). [1]
Іншими словами, g є примітивом стосовно p. Наприклад, якщо р = 11, то 2 – це генератор по модулю 11:
210 = 1024º1 (mod 11)
21 = 2 º 2 (mod 11)
28 = 256 º 3 (mod 11)
22 = 4 º 4(mod 11)
24 =16 º 5(mod 11)
29 = 512 º 6 (mod 11)
27 = 128 º 1 (mod 11)
23 = 8 º 8(mod 11)
26 = 64 º 9(mod 11)
25 = 32 º 10 (mod 11)
Кожне число від 1 до 10 може бути представлено як 2a(mod p). Для р=11 генераторами є 2, 6, 7 і 8. Інші числа не є генераторами. Наприклад, генератором не є число 3, тому що не існує рішення для
3a º 2(mod 11)
У загальному випадку перевірити, чи є дане число генератором, нелегко. Однак задача спрощується, якщо відомо розкладання на множники для p – 1. Нехай q1, q2, ... , qn – це різні прості множники p – 1. Щоб перевірити, чи є число g генератором по модулю p, обчисліть
для всіх значень q=q1, q2,..., qn.
Якщо це число дорівнює 1 для деякого q, то g не є генератором. Якщо для всіх значень q розраховане значення не дорівнює 1, то g – генератор. [1]
Приклад 3.10.1. Нехай p = 11. Прості множники р – 1 = 10 – це 2 і 5. Для перевірки того, чи є число 2 генератором, обчислимо:
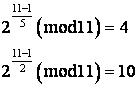
Жодна з відповідей не дорівнює 1, тому 2 – це генератор.
Приклад 3.10.2. Перевіримо, є чи генератором число 3:
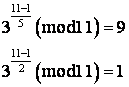
Отже, 3 – це не генератор.
Розкласти число на множники – значить знайти його прості співмножники.
10 = 2×5
60 = 2×2×3×5
252601=41×61×101
2113 – 1 =3391×23279×65993×1868569×1066818132868207
Розкладання на множники є однією з найдавніших проблем теорії чисел. Цей процес нескладний, але вимагає часу. Це поки залишається так, але ряд зрушень у цьому мистецтві усе-таки відбувся.
Приведемо перелік найбільш вдалих алгоритмів факторизації: [1]
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.