Учбово-методичний посібник для виконання лабораторних робіт з дисципліни „Основи теорії криптографії і криптоаналізу”, страница 45

Багатоалфавітні шифри відрізняються від одноалфавітних тим, що одному символу відкритого тексту в різних позиціях може відповідати декілька різних символів в залежності від ключа. Цей факт значно посилює криптостійкість шифрів перед статистичним аналізом, тому що розподілення частот символів в шифртексті стає більш однорідним. [5]

Теоретичні відомості

Так званий шифр Гронсфельда складається в модифікації шифру Цезаря числовим ключем. Для цього під повідомленням пишуть ключ. Якщо ключ коротше повідомлення, то його повторюють циклічно.

Спробуємо скласти таблицю імовірностей зустрічі у відкритому тексті того, чи іншого символу. Імовірність визначаємо за формулою:

,

де N_i – кількість символів L_i у тексті; L – загальна кількість “відомих” символів у тексті.

Текст для аналізу:

НА_СЬОГОДНІШНІЙ_ДЕНЬ_ВІДОМО_БАГАТО_МЕТОДІВ_ШИФРУВАННЯ_В_ЯКИХ_ВИКОРИСТОВУЮТЬСЯ_ВИПАДКОВІ_ЧИСЛА_В_РІЗНИХ_АЛГОРИТМАХ_ВОНИ_МОЖУТЬ_МАТИ_РІЗНЕ_ПРИЗНАЧЕННЯ_НА_ЇХ_ОСНОВІ_ГЕНЕРУЮТЬСЯ_КЛЮЧІ_АБО_НА_ОСНОВІ_КОРОТКОГО_КЛЮЧА_ЩО_ЗАДАЄ_КОРИСТУВАЧ_ГЕНЕРУЄТЬСЯ_ІНШИЙ_СКЛАДНИЙ_КЛЮЧ_ПОТРІБНИЙ_ДЛЯ_ДАНОГО_АЛГОРИТМУ_АЛЕ_В_ЦІЛОМУ_ЗНАЮЧИ_ЦІ_ЧИСЛА_МОЖНА_ПОВНІСТЮ_ЧИ_ЧАСТКОВО_РОЗКРИТИ_ШИФРОВАНЕ_ПОВІДОМЛЕННЯ_ЩО_НЕ_Є_ДОБРЕ_ТОМУ_В_КРИПТОГРАФІЇ_ВЕЛИКУ_УВАГУ_ПРИДІЛЯЮТЬ_ЯКОСТІ_ВИКОРИСТОВУЄМОГО_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ_ГЕНЕРАТОРА_ВИПАДКОВИХ_ЧИСЕЛ_ПІД_ЯКІСТЮ_БУДЬ_ЯКОГО_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ_РОЗУМІЮТЬ_СТУПІНЬ_ЗАЛЕЖНОСТІ_ГЕНЕРОВАНОГО_ВИПАДКОВОГО_ЧИСЛА_ВІД_ПОПЕРЕДНЬОГО_ВИДАНОГО_ЦИМ_ЖЕ_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ_В_ІДЕАЛЬНОМУ_ВИПАДКУ_ЧИСЛА_ЩО_ВИДАЮТЬСЯ_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ_НЕ_ПОВИННІ_БУТИ_ЗВЯЗАНІ_МІЖ_СОБОЮ_ЯКБИ_ТАК_БУЛО_ТО_ЗЛОЧИНЕЦЬ_НАВІТЬ_ЗНАЮЧИ_ЧАСТИНУ_ВИПАДКОВИХ_ЧИСЕЛ_НЕ_ЗМІГ_БИ_ДАЛІ_ДЕШИФРУВАТИ_ЖОДНОГО_НАСТУПНОГО_ВИПАДКОВОГО_ЧИСЛА_ТОБТО_ШИФРУВАННЯ_БУЛО_Б_АБСОЛЮТНО_НАДІЙНИМ_РЕАЛЬНО_Ж_ОТРИМАТИ_ІДЕАЛЬНИЙ_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ_ВАЖКО_ХОЧА_І_МОЖЛИВО_ЦЕ_МОЖНА_ЗРОБИТИ_НАПРИКЛАД_НА_ОСНОВІ_ПРИЛАДУ_ЩО_ПЕРЕВОДИТЬ_У_ПОТРІБНУ_ФОРМУ_АБСОЛЮТНО_ВИПАДКОВУ_ШВИДКІСТЬ_ВІТРУ_У_ДАНОМУ_МІСЦІ_АБО_НА_ОСНОВІ_ПЕРЕВОДУ_У_ЧИСЛА_ІНТЕРВАЛІВ_МІЖ_НАТИСКАМИ_КОРИСТУВАЧА_НА_КНОПКИ_КЛАВІАТУРИ_ПЕРСОНАЛЬНОГО_КОМПЮТЕРА_ТЕЖ_АБСОЛЮТНО_ВИПАДКОВІ_ПОСЛІДОВНОСТІ_ЯКЩО_ЗАДАТИ_ОДИНИЧНИЙ_ІНТЕРВАЛ_ДОСТАТНЬО_МАЛИМ_АЛЕ_ОСНОВНА_ПРОБЛЕМА_НЕ_В_ПРОЦЕСІ_ОТРИМАННЯ_НЕЗАЛЕЖНИХ_ВИПАДКОВИХ_ЧИСЕЛ_БАГАТО_ШИФРОВОК_ПРОСТО_НЕ_ЗМОЖУТЬ_БУТИ_РОЗШИФРОВАНІ_ЗАКОННИМИ_КОРИСТУВАЧАМИ_ЯКЩО_ЗАШИФРОВАНІ_СПРАВЖНІМ_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ

Таблиця 15.1. Розподілення імовірностей появи символів у відкритому тексті

Проаналізуємо цю таблицю. Найчастішим символом у будь-якому тексті є пробіл (його імовірність становить десь 14-19%), інші символи (О, А, Е, І) дещо менш імовірні (десь 5-10%). Тому ми можемо зробити висновок, що найчастіші символи у тексті, зашифрованому за допомогою шифру Гронсфельда, отримані переважно з пробілу. Якщо використовувався ключ,

,

а код пробілу в алфавіті дорівнює 1, то найчастішими символами у шифрованому тексті будуть символи:

.

Однак через те, що ключ накладається на повідомлення циклічно, символ може бути отриманий з символів:

,

але їх імовірності значно менше імовірностей пробілу, тому вони накладають на перетворення невелике викривлення. Взагалі сума імовірностей отриманих символів дорівнює:

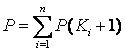
При цьому, якщо Р(1) – імовірність пробілу у відкритому тексті, то Р>Р(1). Однак, якщо ми знайдемо відношення , то побачимо, що при однаковому n (довжина ключа) для різних текстів .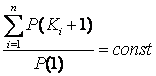

Таким чином, знаючи межі зміни елементів ключа K_i, а також розподілення імовірностей символів у цих межах, ми можемо знайти елементи ключа, вибираючи перші n найчастіших символів.

Для того, щоб розрахувати довжину ключа, проаналізуємо розподілення імовірностей перших k (межі зміни елементів ключа K_i) символів, починаючи від базового (в найпростішому випадку k=10, базовий символ – пробіл).

Використаний при шифруванні алфавіт:

Шифрований текст (код 314)