Учбово-методичний посібник для виконання лабораторних робіт з дисципліни „Основи теорії криптографії і криптоаналізу”, страница 49

Отже в результаті матимемо два ASCII-символи, що відповідають “@” та “ю”. При розшифровці використовуємо ту ж саму операцію накладання XOR: накладаємо на шифровку генеруєму гаму (що ідентична гамі, накладеній при шифруванні) і в результаті маємо вихідний текст:

10000000 00111111

11000000 11000001 ® 192₁₀, 193₁₀ ® АБ

Нагадаємо, що операція XOR бінарна (тобто виконується над двома операндами), обратима і її значення приводимо в таблиці істинності:

Таблиця 17.1. Таблиця істинності

Простою мовою XOR можна охарактеризувати як “або те, або те, але не те і те разом”.

Отже (повертаємось до завдання на лабораторну роботу), маємо перехоплену шифровку довжиною 36 байт, тобто 36 ASCII-символів. Супротивник україномовний і так як вихідний документ цілком таємний, то починається він словами “ЦІЛКОМ ТАЄМНО”. Нам відомо, що передається код доступу, отже можемо припустити, що далі йдуть слова “КОД ДОСТУПУ”, після яких йде саме код доступу в чисельній формі. Кінцево текст мав вигляд: “ЦІЛКОМ ТАЄМНО КОД ДОСТУПУ ХХХХ”, де замість ХХХХ має бути шуканий код. Отже, кінцевим завданням є знаходження коду доступу, що є різним для всіх варіантів (весь інший текст однаковий для всіх варіантів). Ми відвели 4 розряди під код, бо об‘єм шифровки відомий (36 символів), і відомих символів є 32. Отже для кожного варіанта дається шифровка у вигляді 36 чисел (які являють собою коди ASCII). По ним треба знайти код доступу у числовій формі, наприклад “1234”. Для того, щоб завдання не здавалось надуманим, нагадаємо, що файли будь-яких форматів містять заголовок у якому є фіксовані слова або числа. Наприклад, всі звукові WAV-файли починаються з літер “RIFF”. Причому таких місць у будь-яких файлах (можливо крім текстових) предостатньо. Тому шифруючи такі файли різними алгоритмами (без перестановок) завжди знатимемо, які тут мають бути символи, а отже зможемо встановити деякі відповідності між вихідним текстом (в даному випадку із байт) і шифровкою, що, безперечно послаблює стійкість шифрів. Єдиним висновком для захисників інформації є необхідність обов‘язкового застосування алгоритмів перестановки після шифрування базовим алгоритмом.

Послідовність дій для дешифрації:

1) Визначення перших 32 символів гами. Ми можемо це зробити, адже ми знаємо перші 32 символи вихідного тексту (“ЦІЛКОМ ТАЄМНО КОД ДОСТУПУ”) і 32 символи шифровки. Отже, переводимо всі ASCII-коди шифровки в бінарний вигляд. Це можна зробити за допомогою спеціального калькулятора, комп‘ютерної програми, або методом ділення на двійку у стовпчик. Переводимо також у бінарний вигляд текст “ЦІЛКОМ ТАЄМНО КОД ДОСТУПУ”. Його представлення в ASCII-кодах: 214, 178, 203, 202, 206, 204, 32, 210, 192, 170, 204, 205, 206, 32, 202, 206, 196, 32, 196, 206, 209, 210, 211, 207, 211,. Переведення в бінарний вигляд шляхом ділення у стовпчик на 2 розглянемо для прикладі на числа 473:

Операція div – позначає ділення націло. Ділення ведемо доки ціла частина від ділення не стане дорівнювати 0. Потім виписуємо залишки у зворотному порядку і отримаємо бінарний еквівалент числа. Отже 473₁₀ = 111011001₂. Але замість ручного переводу краще все ж скористатися калькулятором з вбудованою функцією переводу в бінарну систему (ділення в стовпчик займає надто багато часу).

Коли ми маємо бінарний вигляд шифровки і відомого тексту, застосовуємо операцію XOR. Для цього виписуємо послідовність біт шифровки у строку (намагаємось групувати їх по 8, щоб легше було орієнтуватися де початок наступного байта), а під нею послідовність біт відомого тексту (теж у групах по 8). Для кожного біта шифровки застосовуємо XOR з відповідним бітом відомого тексту. Приклад операції XOR показано вище. Після виконання цієї операції матимемо послідовність біт гами. Розбиваємо її на групи по 8 біт, повинні отримати 32 восьмирозрядних груп біт. Кожна така група являє собою якесь число в діапазоні 0..255, яке було генероване ПВЧ супротивника. Переводимо ці восьмирозрядні бінарні групи в десяткову форму. Наприклад, маємо послідовність біт гами:

10001000 01011000 …(ще 30 груп по 8 біт)

Беремо першу групу з 8 біт і переводимо її в десятковий вигляд:

1×2⁷ + 0×2⁶ + 0×2⁵ + 0×2⁴ + 1×2³ + 0×2² + 0×2¹ + 0×2⁰ = 128 + 8 = 136; друга:

0×2⁷ + 1×2⁶ + 0×2⁵ + 1×2⁴ + 1×2³ + 0×2² + 0×2¹ + 0×2⁰ = 64 + 16 + 8 = 88; і т.д.

Отже кінцево маємо послідовність 32 чисел генерованих ПВЧ. Спробуємо спрогнозувати на основі цього які наступні 4 числа були ним видані. Якщо це нам вдасться, то ми зможемо знайти код доступу, наклавши ці 4 числа на останні 4 байти шифровки за допомогою XOR!

Для дослідження псевдовипадкової послідовності спробуємо виділити її тренд методом найменших квадратів. Тренд – це функціональна залежність, яка приблизно показує поведінку псевдовипадкової послідовності. Наведемо приклад. Маємо послідовність чисел 9, 4, 1. Її можна добре апроксимувати як параболу (і – 4)², графік приведений на рисунку.

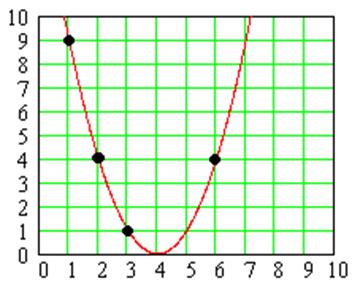
Рис.17.1. Тренд послідовності 9, 4, 1.

Знаючи тренд (і – 4)² можна за допомогою екстраполяції прогнозувати значення наступних випадкових чисел (наприклад через три кроки генератор вірогідніше за все видасть 4).