Учбово-методичний посібник для виконання лабораторних робіт з дисципліни „Основи теорії криптографії і криптоаналізу”, страница 15

Доказ. Нехай (c, b) = d. Маємо: d|b, d|c, отже d|ac, тобто d – дільник ас і b. Нехай тепер (ac, b) = s. Маємо: s|b, s|ac, s – дільник b, тобто або s = 1, або s не поділяє а. Це означає, що s|c, значить s|d. Отже, d і s поділяються один на одного, тобто d = s.

Одним зі способів обчислити найбільший загальний дільник двох чисел є алгоритм Евкліда. От як він виглядає при його описі мовою C++ [5]:

unsigned long NOD(unsigned long x,unsigned long y)

{

unsigned long z=0;

while(x>0)

{

z=x;

x=y%x;

y=z;

}

return z;

}

Кнут у своїй книзі «Искусство программирования» [13] приводить т.зв. розширений алгоритм Евкліда, призначений для рішення діофантових рівнянь першого ступеня виду: ax+by=c, де a, b, c – задані константи (видно, що розширений алгоритм Евкліда будується на основі властивості 3.3.1.).

Розширений алгоритм Евкліда мовою C++ можна описати в такий спосіб:

void Extended_Euclid(long &a,long &b,long &x,long &y,long &NOD)

{

if(a<b)Swap(a,b);

long q,r,x1,x2,y1,y2;

if(b==0)

{

NOD=a;

 x=1;

 y=0;

 return;

 }

 x2=1,x1=0,y2=0,y1=1;

while(b>0)

{

 q=a/b;r=a%b;

 x=x2-q*x1;

 y=y2-q*y1;

 a=b;b=r;

 x2=x1;x1=x;y2=y1;y1=y;

}

NOD=a;

x=x2;

y=y2;

}

1.3.4.  Теорія порівнянь.

Визначення 3.4.1. Нехай а, b ÎZ, m ÎN. Говорять, що число а порівнянне з b по модулю m, якщо а і b при розподілі на m дають однакові залишки. Запис цього факту виглядає так: a ºb (mod m). [11]

Перелічимо, далі, властивості порівнянь, схожі на властивості рівнянь.

Властивість 3.4.1. Порівняння по однаковому модулю можна почленно додавати. [11]

Доказ. Нехай a₁ºb₁(mod m), a₂ºb₂(mod m). Це означає, що a₁=b₁+mt₁, a₂ =b₂ +mt₂. Після додавання останніх двох рівностей одержимо a₁+a₂=b₁+b₂+m (t₁+t₂), що означає a₁+a₂ ºb₁+b₂ (mod m).

Властивість 3.4.2. Доданок, що знаходиться в якій-небудь частині порівняння, можна переносити в іншу частину, змінивши його знак на протилежний. [11]

Доказ.

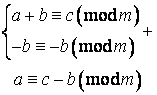
Властивість 3.4.3. До будь-якої частини порівняння можна додати будь-яке число, що кратне модулю. [11]

Доказ.

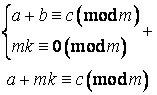
Властивість 3.4.4. Порівняння по однаковому модулю можна почленно перемножувати. [11]

Доказ.

Властивість 3.4.5. Обидві частини порівняння можна звести в одну й ту саму ступінь. [11]

Доказ. Для доказу достатньо використати необхідну кількість разів властивість 3.4.4.

Як наслідок з перерахованих вище властивостей, одержуємо наступну властивість:

Властивість 3.4.6. Якщо a₀ ºb₀ (mod m), a₁ ºb₁ (mod m),..., a_n ºb_n (mod m), x ºy (mod m), то a₀ xⁿ +a₁ x^n-1 +...+a_n ºb₀ yⁿ +b₁ y^n-1 +...+b_n (mod m) [11]

Властивість 3.4.7. Обидві частини порівняння можна розділити на їхній загальний дільник, взаємно простий з модулем. [11]

Доказ. Нехай a ºb (mod m), a=a₁d, b=b₁d. Тоді (a₁ – b₁)×d поділяється на m. Оскільки d і m взаємно прості, то на m поділяється саме (a₁ – b₁), що означає a₁ ºb₁(mod m).

Властивість 3.4.8. Обидві частини порівняння і його модуль можна помножити на одне й те саме ціле число або розділити на їхній загальний дільник. [11]

Доказ.

a ºb(mod m) Û a=b+mt Û ak=bk+mkt Ûak ºbk(mod mk).

Властивість 3.4.9. Якщо порівняння a ºb має місце по декількох різних модулях, то воно має місце і по модулю, рівному найменшому загальному кратному цих модулів. [11]

Доказ. Якщо a ºb(mod m₁) і a ºb(mod m₂), то a – b поділяється на m₁ і на m₂, значить a – b поділяється на найменше загальне кратне m₁ і m₂.

Властивість 3.4.10. Якщо порівняння має місце по модулю m, то воно має місце і по модулю d, рівному будь-якому дільникові числа m. [11]

Доказ очевидний випливає з транзитивності відносини подільності: якщо a ºb (mod m), то a – b поділяється на m, значить a – b поділяється на d, де d|m.

Властивість 3.4.11. Якщо одна частина порівняння і модуль поділяються на деяке число, то й іншу частину порівняння потрібно поділити на те ж число. [11]

Доказ.

a ºb (mod m) Û a=b+mt. Припустимо, b і m поділяються на одне число (наприклад, n), тоді bº0 (mod n), mº0 (mod n). Одержуємо b+mtº0 (mod n), тобто аº0 (mod n).

1.3.5.  Повна система відрахувань.

Відношення порівнянності по довільному модулю m є відношення еквівалентності на множині цілих чисел. Це відношення еквівалентності ініціює розбивку множині цілих чисел на класи еквівалентних між собою елементів, тобто в один клас поєднуються числа, що дають при розподілі на m однакові залишки. Число класів еквівалентності в точності дорівнює m.

Визначення 3.5.1. Будь-яке число з класу еквівалентності будемо називати відрахуванням по модулю m. Сукупність відрахувань, узятих по одному з кожного класу еквівалентності, називається повною системою відрахувань по модулю m (у повній системі відрахувань, таким чином, усього m штук чисел). Безпосередньо самі залишки при розподілі на m називаються найменшими додатними відрахуваннями і, звичайно, утворять повну систему відрахувань по модулю m. Відрахування rназивається абсолютно найменшим, якщо ïrïнайменший серед модулів відрахувань даного класу.

Лема 3.5.1. 1) Будь-які m штук попарно не порівнянних по модулю m чисел утворять повну систему відрахувань по модулю m. [11]

2) Якщо а і m взаємно прості, а x пробігає повну систему відрахувань по модулю m , то значення виду ах+b , де b – будь-яке ціле число, теж пробігають повну систему відрахувань по модулю m.

Доказ. Твердження 1) – очевидно. Доведемо твердження 2). Чисел ах+b рівно m штук. Покажемо, що вони між собою не порівнянні по модулю m. Ну нехай для деяких різних x₁ і x₂ з повної системи відрахувань виявилося, що ax₁+b ºax₂+b(mod m). Тоді, по властивостях порівнянь з попереднього пункту, одержуємо:

ax₁ ºax₂ (mod m)

x₁ ºx₂ (mod m)

– протиріччя з тим, що x₁ і x₂ різні й узяті з повної системи відрахувань.