Учбово-методичний посібник для виконання лабораторних робіт з дисципліни „Основи теорії криптографії і криптоаналізу”, страница 41

де: 32 – число літер українського алфавіту.

Виражене як відсоток,  – ледве більше 3%. Говорячи іншими словами, при 100 вибірках збіг символів відбувається в середньому 3,125 рази.

Якщо ви вибираєте два символи зі звичайного українського тексту, то імовірність їхнього збігу виявляється більшою, ніж  (через нерівномірність розподілу частот символів). Вивчення частот показує, що імовірність збігу символів у звичайному українському тексті сягає величини 0,05825. Говорячи іншими словами, при 100 вибірках збіг символів відбувається в середньому 5,825 рази [7]. Кожна мова має свої власні імовірності збігу символів, але подібні закономірності мають місце в кожному алфавіті.

Різні іспити збігу використовують різні методи порівняння символів один з одним, але кожний спирається на порівняння імовірностей збігу для випадкового і звичайного тексту. Фактичне число збігів у криптограмі може бути зрівняне з імовірностями збігу для випадкового і звичайного тексту, щоб зробити висновок про метод шифрування, застосований в даній шифровці.

Індекс відповідності

Звичайний спосіб вираження результатів іспиту збігу – індекс відповідності (ІВ). Індекс відповідності – відношення фактичних збігів у ході іспиту до числа, очікуваному у випадковому розподілі. Для звичайного тексту, очікуваний індекс відповідності для окремих символів українського алфавіту – відношення = 1,864 [9].

Монограмний PHI-тест

Найбільш загальний випадок іспиту збігу – монограмний PHI-тест, що забезпечує математичний шлях виміру нерівномірності розподілу частоти. Монограма –синонім одного символу. Необхідно відрізняти монограмний PHI-тест від PHI-тесту взагалі (зокрема, від біграмного PHI-тесту, виконуваного для пар символів). PHI – запис в англійській транскрипції грецького символу F. Монограмний PHI-тест заснований на імовірностях збігу, що відбуваються, коли кожен символ у криптограмі порівнюється з кожним іншим символом.

Для проведення PHI-тесту може бути розраховане без фактично порівняння кожного символу з кожним іншим символом. Загальна кількість порівнянь і загальна кількість збігів може бути розрахована виходячи тільки з розподілу частоти.

Загальна кількість порівнянь, коли кожен символ порівнюється з кожним іншим символом виражається формулою:

Знаючи кількість іспитів і очікуване значення імовірності в кожному окремому іспиті знаходимо загальне очікуване значення для відкритого тексту:

і випадкового тексту:

Також, як і загальна кількість порівнянь – N(N-1), загальна кількість збігів для кожного символу – f(f-1), де f – число символів у тексті. Загальна кількість збігів – сума збігів для всіх символів. Загальну кількість збігів позначають Ф_О (PHI очікуваний):

Індекс відповідності для PHI-тесту позначається DIC. DIC – відношення PHI, очікуваного до PHI випадкового:

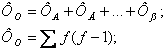Пояснимо проведення PHI-тесту на прикладі

Звичайний текст:

РІЗНІ ІСПИТИ ЗБІГУ ВИКОРИСТОВУЮТЬ РІЗНІ МЕТОДИ ПОРІВНЯННЯ СИМВОЛІВ ОДИН З ОДНИМ АЛЕ КОЖНИЙ СПИРАЄТЬСЯ НА ПОРІВНЯННЯ ІМОВІРНОСТЕЙ ЗБІГУ ДЛЯ ВИПАДКОВОГО І ЗВИЧАЙНОГО ТЕКСТУ ФАКТИЧНЕ ЧИСЛО ЗБІГІВ У КРИПТОГРАМІ МОЖЕ БУТИ ЗРІВНЯНЕ З ІМОВІРНОСТЯМИ ЗБІГУ ДЛЯ ВИПАДКОВОГО І ЗВИЧАЙНОГО ТЕКСТУ ЩОБ ЗРОБИТИ ВИСНОВОК ПРО МЕТОД ШИФРУВАННЯ ЯКЩО ВИ ВИБИРАЄТЕ БУДЬ ЯКІ ДВА СИМВОЛИ З ПОВІДОМЛЕННЯ ПОРІВНЮЄТЕ ЇХ РАЗОМ І ВОНИ ВИЯВЛЯЮТЬСЯ ОДНАКОВИМИ ТО ГОВОРЯТЬ ЩО ЦІ СИМВОЛИ ЗБІГАЮТЬСЯ

	А	Б	В	Г	Д	Е	Є	Ж	З	И	І
f	15	10	31	11	12	12	3	2	15	34	27
f-1	14	9	30	10	11	11	2	1	14	33	26
f(f-1)	210	90	930	110	132	132	6	2	210	1122	702
	Ї	Й	К	Л	М	Н	О	П	Р	С	Т
f	1	4	12	9	14	27	46	10	18	15	22
f-1	0	3	11	8	13	26	45	9	17	14	21
f(f-1)	0	12	132	72	182	702	2070	90	306	210	462
	У	Ф	Х	Ц	Ч	Ш	Щ	Ь	Ю	Я
f	10	2	1	1	4	1	3	6	4	18
f-1	9	1	0	0	3	0	2	5	3	17
f(f-1)	90	2	0	0	12	0	6	30	12	306

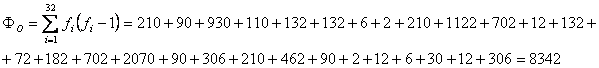
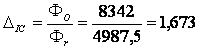
Одноалфавітна заміна

УКЇРККФТЙХЙЇДКЄЦЕЙНСУЙФХСЕЦБХАУКЇРКПЗХСЖЙТСУКЕРВРРВФЙПЕСОКЕСЖЙРЇСЖРЙПГОЗНСІРЙМФТЙУГИХАФВРГТСУКЕРВРРВКПСЕКУРСФХЗМЇДКЄЦЖОВЕЙТГЖНСЕСЄСКЇЕЙЬГМРСЄСХЗНФХЦЧГНХЙЬРЗЬЙФОСЇДКЄКЕЦНУЙТХСЄУГПКПСІЗДЦХЙЇУКЕРВРЗЇКПСЕКУРСФХВПЙЇДКЄЦЖОВЕЙТГЖНСЕСЄСКЇЕЙЬГМРСЄСХЗНФХЦЯСДЇУСДЙХЙЕЙФРСЕСНТУСПЗХСЖЮЙЧУЦЕГРРВВНЯСЕЙЕЙДЙУГИХЗДЦЖАВНКЖЕГФЙПЕСОЙЇТСЕКЖСПОЗРРВТСУКЕРБИХЗЛШУГЇСПКЕСРЙЕЙВЕОВБХАФВСЖРГНСЕЙПЙХСЄСЕСУВХАЯСЩКФЙПЕСОЙЇДКЄГБХАФВ