Постановка задач механики деформируемого твердого тела и схемы их решения. Условия связности многосвязного тела, страница 9

Доказательство единственности решения уравнений теории упругости проводится стандартным для линейных уравнений методом, путем доказательства отсутствия решения однородной системы уравнений при однородных краевых условиях.

Для разности решений уравнения равновесия (5.40) имеют вид:  Умножим его на u_i и проинтегрируем по объему. Получим

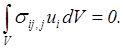
Заметив, что , преобразуем этот интеграл, применив формулу Гаусса-Остроградского,

.

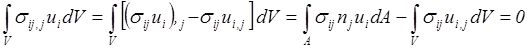Поверхностный интеграл равен нулю вследствие условий на поверхности, см. (5.45). В результате оказывается, что

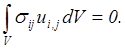
Так как  то

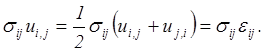
Поэтому последний интеграл запишется в виде

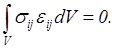
Подынтегральное выражение с помощью закона Гука (5.42) пре образуется следующим образом

см. (4.22). Тогда имеем

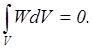
Но интеграл по объему от положительно определенной функции, каковой является упругий потенциал W, равен нулю только тогда, когда эта функция равна нулю во всех точках объема. Последнее возможно только тогда, когда везде равны нулю компоненты тензоров деформаций ε_ij, см. (4.22). Таким образом, нулевым краевым условиям могут соответствовать только нулевые решения. Этим и доказывается теорема единственности.

Заметим, что при решении первой основной задачи перемещения определяются с точностью до смещения тела как жесткого целого. Дело в том, что равенство нулю компонентов тензора деформаций ε_ij не означает равенства нулю компонентов перемещения u_i. Деформации отсутствуют и при перемещении тела как жесткого целого, т.е. при выполнении равенств

    

где  Однако такое различие в решении задач теории упругости считается не существенным. В случаях решения второй и смешанных задач исчезает и это различие, поскольку перемещения заданы заранее на всей или части поверхности тела.

5.3.3. Уравнения теории упругости в перемещениях

Уравнения теории упругости (5.40)-(5.42) можно привести к системе трех уравнений, разрешаемых относительно компонент перемещения. Для этого поступим следующим образом. Подставим уравнения (5.41) в (5.42):

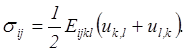                                            (5.46)

Внесем (5.46) в уравнения (5.40). В результате получим искомую систему уравнений

                                           (5.47)

Уравнения (5.47) образуют систему дифференциальных уравнений общего шестого порядка.

Для изотропного тела

и система уравнений (5.47) приводится к виду

                                         (5.48)

где , а ∆ – дифференциальный оператор Лапласа, .

Система дифференциальных уравнений (5.48) введена в теорию упругости французским ученым Ламе (1833 г.) и носит его имя.

При решении большинства задач теории упругости объемные силы принимаются равными нулю, F_i=0. Дело в том, что объемные силы во многих случаях оказывают малое влияние на напряженно-деформированное состояние тела. С другой стороны они обычно выражаются весьма простыми функциями от координат, в силу чего нахождение частного решения уравнений (5.48) не вызывает особых затруднений. После нахождения частного решения, видоизменяются краевые условия, которые ставятся уже для однородной системы уравнений (5.48) при F_i=0. Нахождение решения этой системы уравнений при заданных краевых условиях составляет основную трудность при решении задач теории упругости.

На основании уравнений (5.48) можно легко установить, что каждая из компонент перемещений является бигармонической функцией. Для этого достаточно, приняв F_i=0, продифференцировать каждое уравнение (5.48) по координате x_i и сложить их между собой. Тогда получим ∆θ=0, т.е. объемное расширение упругого изотропного тела при отсутствии объемных сил представляет собой гармоническую функцию. Взяв теперь оператор Лапласа от уравнений (5.48) при F_i=0 убедимся в том, что каждая компонента перемещений является бигармонической функцией, ∆∆u_i=0.

Уравнения теории упругости в перемещениях могут быть решены при любых краевых условиях. Если краевые условия сформулированы в силах (первая основная и смешанная задачи), то следует по закону Гука выразить напряжения через компоненты тензора деформации, а затем с помощью уравнений (5.41) - через первые производные компонентов перемещения. В результате решения уравнений теории упругости в перемещениях, находятся компоненты перемещения, зная которые, по формулам (5.41) определяют компоненты тензора деформаций. После этого с помощью уравнений закона Гука находятся компоненты тензора напряжений.