![]() . (5.28)
. (5.28)
Отсюда приходим к выводу, что существует такой функционал
![]() (5.29)
(5.29)
который в реально осуществляющихся процессах принимает стационарное значение, т.е. δJ=0. Таким образом, в реально осуществляющихся процессах деформирования сплошной среды функционал (5.29) принимает стационарное значение и обращается в вариационное уравнение (5.28), выражающее собой уравнение баланса механической энергии для возможных приращений определяющих функций.
Приращения определяющих функций ![]() ,
, ![]() ,
, ![]() ,
и
,
и ![]() известны, см.
(3.63), (3.68), (3.64), (3.66). Заменяя символ действительного приращения на
символ допустимого приращения, получим
известны, см.
(3.63), (3.68), (3.64), (3.66). Заменяя символ действительного приращения на
символ допустимого приращения, получим
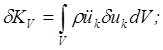
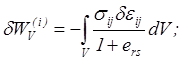
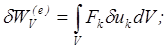
![]() .
.
В результате вариационное уравнение (5.28) примет вид
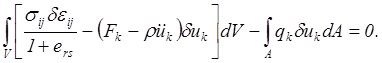 (5.30)
(5.30)
Введя обозначение
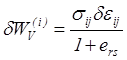 ,
(5.31)
,
(5.31)
приведём функционал (5.29) к следующей форме
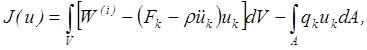 (5.32)
(5.32)
где в качестве независимых функциональных аргументов принимаются компоненты перемещений сплошной среды.
Вариационное уравнение (5.30),
рассматриваемое как утверждение о
стационарности функционала J(u) (5.32) в реально осуществляющихся
процессах деформирования, носит название принципа Даламбера. При статических процессах
деформирования инерционные силы равны нулю: ![]() и
уравнение (5.30) представляет собой принцип возможных перемещений или принцип Лагранжа
(функционал J(u) в этом случае носит имя Лагранжа).
и
уравнение (5.30) представляет собой принцип возможных перемещений или принцип Лагранжа
(функционал J(u) в этом случае носит имя Лагранжа).
Вариационное уравнение (5.30) отличается от уравнения баланса механической энергии (3.69) лишь символами приращений. А так как математические операции, выражаемые этими символами, совершенно одинаковы, то результат применения вариационного уравнения (5.30) к задачам механики деформируемого твердого тела ничем не отличается от результата использования уравнения (3.69). Отсюда следует, что непосредственное применение вариационного уравнения (5.30) позволяет получать уравнения движения сплошной среды и краевые условия, см. п. 5.1.2. Это означает, что истинные перемещения сплошной среды реализуются только при полном удовлетворении уравнений движения (равновесия) внутри тела и уравнений равновесия на ограничивающих его поверхностях.
Принципы Даламбера и возможных перемещений являются самыми общими принципами механики сплошных сред. Применительно к различным классам сплошных сред разрабатываются свои специфические вариационные принципы. Наибольшим разнообразием отличаются упругие тела.
Вариационные принципы Даламбера и Лагранжа (принцип возможных перемещений) полностью применимы к задачам теории упругости. Более того, на базе этих принципов можно получить новые вариационные принципы теории упругости. Поскольку упругие свойства материалов проявляются только при малых деформациях, т.е. при еrs<< 1, то введённая обозначением (5.31) определяющая функция W(i) сводится к упругому потенциалу W (4.12), (4.15).
Американский учёный немецкого происхождения Э. Рейсснер, на базе принципа возможных перемещений предложил для теории упругости свой вариационный принцип, выразив упругий потенциал через потенциал деформаций Ф. На основании (4.18) вариация потенциала деформаций равна
![]() (5.33)
(5.33)
Выразив упругий потенциал W через потенциал деформаций, см. вывод формулы (4.18) приведем функционал (5.32) к смешанной форме варьирования по независимым функциональным аргументам ui и σij:
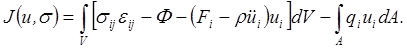 (5.34)
(5.34)
Стационарное значение функционала (5.34) позволяет получить уравнения движения, уравнения состояния и краевые условия упругого тела. Покажем это для случая малых деформаций при малых приращениях перемещений. С помощью уравнений Коши (2.54) получим следующее равенство
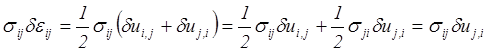
которое используем при определении стационарного значения функционала (5.34). Итак
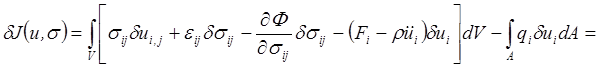
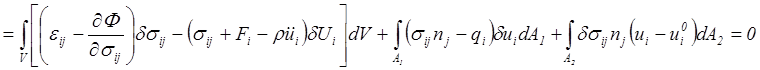 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.