Постановка задач механики деформируемого твердого тела и схемы их решения. Условия связности многосвязного тела, страница 4

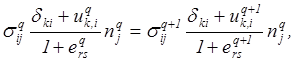
                     (5.12)

Силовые условия сопряжения смежных областей при малых деформациях е_rs << 1 и различных случаях приращения перемещений имеют вид:

-  в общем случае

   ;                            (5.13)

-  в случае малых приращений одинакового порядка

    ;                                      (5.14)

-  в случае, когда приращения перемещений u_3,α являются величинами более низкого порядка малости по сравнению с остальными приращениями перемещений:

    ;        (5.15)

-  в случае, когда приращения перемещений u_2,1 и u_3,1  имеют одинаковый порядок малости, который ниже порядка малости остальных приращений перемещений:

 

        (5.16)

5.1.6. Начальное состояние деформируемого тела

Полная система уравнений деформируемого тела описывает его поведение под воздействием внешней среды. В деформируемом теле ещё до внешнего воздействия могут быть начальные деформации и напряжения, которые являются следствием внутренних процессов формирования твёрдого тела. Например, они могут появиться в результате технологических операций при изготовлении деформируемого тела методом штамповки из-за пластических деформаций. В некоторых случаях начальные деформации и напряжения могут быть определены расчётным методом или экспериментально. Но очень часто они неизвестны. Начальные деформации и напряжения определяют начальное состояние деформируемого тела, которое предшествует его поведению под воздействием внешней среды.

Перемещения всех точек деформируемого тела, появляющиеся в нём дополнительные деформации и напряжения представляют собой реакцию деформируемого тела на внешнее воздействие. Тем самым полная система уравнений деформируемого тела определяет перемещения, деформации и напряжения относительно начального состояния деформируемого тела, т.е. дополнительно к начальным значениям. Полные величины деформаций и напряжений могут быть найдены суммированием их начальных и определённых уравнениями механики деформируемого тела величин. Поэтому при решении уравнений механики деформируемого твёрдого тела, как правило, определение перемещений, деформаций и напряжений производится относительно, так называемого, естественного состояния. Под естественным состоянием понимается начальное состояние, при котором в деформируемом теле начальные деформации и напряжения равны нулю.

5.1.7. Математическое представление постановки задач

механики деформируемого твёрдого тела

Постановка задач механики деформируемого твёрдого тела включает в себя замкнутую систему уравнений механики, краевые и начальные условия. Применительно к многосвязным телам вводятся дополнительные условия сплошности. Для расчёта неоднородных тел дополнительно привлекаются геометрические и силовые условия сопряжения. В декартовой прямоугольной системе координат общая постановка задач механики деформируемого твёрдого тела представляется в виде замкнутой системы уравнений механики:

-  уравнений движения (3.46)

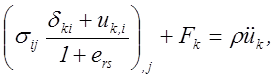
    ;                (5.17)

-  уравнений геометрии сплошных сред (2.9)

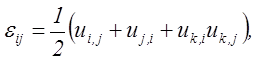
    ;                          (5.18)

-  уравнений состояния упругого или неупругого тела (глава 4)

      ;                                   (5.19)

краевых (5.3), (5.4)

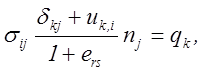
                           (5.20)

                                          (5.21)

и начальных (5.9)

;  ;                  (5.22)

условий.

Применительно к многосвязным телам привлекаются дополнительные условия сплошности (5.11):

                                          (5.23)

а применительно к неоднородным телам вводятся дополнительные условия сопряжения (5.12), (5.11):

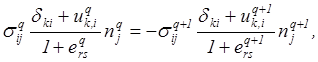
                     (5.24)

                                          (5.25)

В самом общем виде решения задач механики деформируемого твёрдого тела производятся следующим образом. Путём решения системы уравнений (5.17)-(5.19) при краевых (5.20),(5.21) и начальных (5.22) условиях находятся компоненты перемещений, компоненты тензоров напряжений, деформаций и скоростей деформации. Если деформируемое твёрдое тело имеет внутренние замкнутые полости, то для каждой поверхности мнимого разреза, превращяющего многосвязное тело в односвязное, выполняются дополнительные условия сплошности (5.23).