Здесь для преобразования объемного интеграла
использована формула Остроградского-Гаусса и произведено разделение краевой
поверхности на две части, на одной из которых А1
заданы поверхностные силы qi, а на другой А2
перемещения ![]() . При этом вариации перемещений
на краевой поверхности А2 представлены в виде:
. При этом вариации перемещений
на краевой поверхности А2 представлены в виде: ![]() , т.е. как возможные
отклонения от заданных значений
, т.е. как возможные
отклонения от заданных значений ![]() . Так как
вариации перемещений
. Так как
вариации перемещений ![]() и напряжений δσij произвольны и линейно независимы, то последнее равенство выполняется
лишь при условии равенства нулю выражений, стоящих в скобках, при вариациях
перемещений и напряжений. Это обстоятельство позволяет получить уравнения
состояния (4.18) , движения (3.53) и краевые условия (5.6) и (5.4).
и напряжений δσij произвольны и линейно независимы, то последнее равенство выполняется
лишь при условии равенства нулю выражений, стоящих в скобках, при вариациях
перемещений и напряжений. Это обстоятельство позволяет получить уравнения
состояния (4.18) , движения (3.53) и краевые условия (5.6) и (5.4).
Вариационный принцип, основанный на смешанном функционале J(u,σ)(5.34), впервые был предложен Э. Рейсснером для статической теории упругого тела. Поэтому будем называть приведенный здесь вариационный принцип обобщенным принципом Рейсснера.
Для того, чтобы получить полный вариационный принцип, из которого можно было бы вывести полную систему уравнений динамической теории упругости, поступим следующим образом. Внесем в функционал (5.32) при малых деформациях еrs<< 1 слагаемое, тождественно равное нулю, см. (2.54)
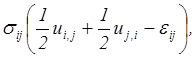
и приведем этот функционал к смешанной
форме варьирования по не зависимым функциональным аргументам ![]() ,
, ![]() ,
, ![]() :
:
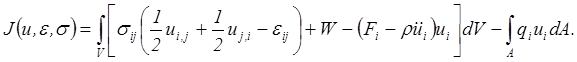 (5.35)
(5.35)
Рассматривая в функционале (5.35)
параметры ![]() ,
, ![]() и
и ![]() как независимые
функциональные аргументы, приравняем нулю вариацию этого функционала
как независимые
функциональные аргументы, приравняем нулю вариацию этого функционала
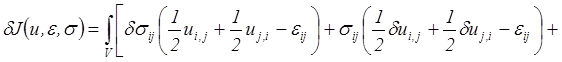
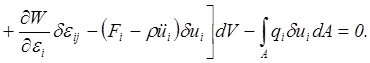
В силу симметрии тензора напряжений, см. п.5.2.2.1.
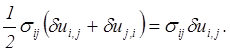
Тогда, воспользовавшись для преобразования объемного интеграла формулой Остроградского-Гаусса, получим
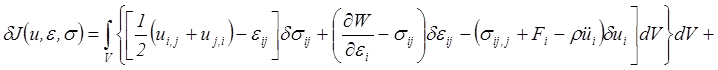
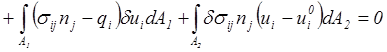 .
.
Так как вариации перемещений δUi, деформаций δεijи напряжений δσij приняты произвольными и линейнонезависимыми друг от друга, то последнее равенство возможно лишь при условии равенства нулю всех выражений, стоящих в скобках в качестве множителей при вариациях. Приравнивая соответствующие выражения нулю, получим уравнения геометрии перемещений сплошной среды (2.54), состояния (4.17), движения (3.53) и краевые условия (5.6) и (5.4). Т.е. получим полную систему уравнений динамической теории упругости вместе с краевыми условиями.
Вариационный принцип, основанный на функционале J(u,ε,σ) (5. 35), в статической теории упругости называется принципом Ху-Вашицу, по именам ученых, впервые предложивших и использовавших его в практической работе. Применительно к динамической теории упругости будем называть его обобщенным принципом Ху-Вашицу.
Широкое распространение в теории упругости получил вариационный принцип Кастильяно, который выведем из функционала Рейсснера (5.34). Для того рассмотрим объемный интеграл, входящий в функционал (5.34),
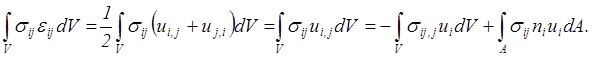
При преобразовании рассматриваемого объемного интеграла использовалось равенство
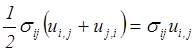 , которое является следствием симметрии
компонентов тензора напряжений, и формула Остроградского-Гаусса.
, которое является следствием симметрии
компонентов тензора напряжений, и формула Остроградского-Гаусса.
В результате подстановки полученного преобразования объемного интеграла приведем функционал (5.34) к виду
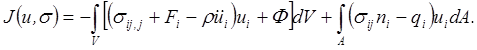
Считая, что уравнения движения и краевые условия на части поверхности А1, где заданы поверхностные силы, полностью удовлетворены, получим функционал, который зависит только от напряжений
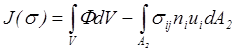 . (5.36)
. (5.36)
Функционал (5.36) называется функционалом Кастильяно. При варьировании функционала (5.36) потребуем, чтобы напряжения были статически и динамически допустимыми, т.е. внутри объема V они должны полностью удовлетворять уравнениям движения (3.48), а на поверхности А1 краевым условиям (5.6). Тогда
![]()
![]() .
.
Вычитая из этих равенств уравнения (3.48) и (5.6), получим
![]()
![]()
![]()
![]() (5.37)
(5.37)
Учитывая, что
![]()
представим вариацию потенциала деформации (дополнительной работы деформации) в виде
![]()
так как внутри упругого тела должны выполняться первые условия (5.37). В результате вариация функционала (5. 36) оказывается равной
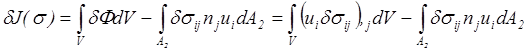 .
.
С помощью формулы Остроградского-Гаусса объемный интеграл сводится к поверхностному
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.