Постановка задач механики деформируемого твердого тела и схемы их решения. Условия связности многосвязного тела, страница 2

Краевые условия отражают условия закрепления краевых поверхностей исследуемого твердого тела и условия нагружения его поверхностными внешними силами, т.е. отражают условия механического воздействия на тело внешней среды. Механическое воздействие внешней среды на деформируемое тело осуществляется через работу, которую совершают внешние объёмные и поверхностные силы на перемещениях, вызванных деформацией тела. В п. 3.9 доказана теорема об изменении кинетической энергии деформируемого тела, которая привела к утверждению, что для любого сплошного тела должно выполняться уравнение баланса механической энергии (3.69). В это уравнение входит работа внешних сил, которую они совершают, деформируя сплошное тело. Поэтому уравнение баланса механической энергии может быть использовано для вывода краевых условий. Более того, выведенные таким образом краевые условия окажутся в полном соответствии с законами природы.

Уравнение баланса механической энергии (3.69) получено применительно к любому индивидуальному объёму конечной величины. Это означает, что оно применимо также для объёма деформируемого тела в целом. При выводе краевых условий под объёмом V будем понимать объём всего тела, под А – его поверхность, а поверхностные силы обозначим через q:  , где  – проекции плотностей поверхностных ил на недеформируемые оси лагранжевой системы координат. В общем случае работа поверхностных сил зависит  от условий воздействия внешней среды на деформируемое тело. Внешние силы, прикладываемые к деформируемому телу, могут быть консервативными, т.е. такими, что их работа не зависит от траекторий перемещения точек приложения и определяется только начальным и конечным положением этих точек, а могут быть неконсервативными, когда такая зависимость существуют. Зависимость работы неконсервативных сил от траекторий перемещения точек их приложения определяется условиями воздействия на рассматриваемое тело  внешней среды. Эти условия могут быть самыми разными и от их правильного отображения зависит точность решения краевой задачи механики деформируемого тела. Здесь мы ограничимся рассмотрением консервативных сил. Работа неконсервативных сил рассматривается в курсах специальных дисциплин. Учитывая полученные ранее выражения для кинетической энергии (3.63), работы объёмных (3.64) и поверхностных (3.66) консервативных сил, а также работы внутренних сил (3.68) представим уравнение баланса механической энергии (3.69) в виде:

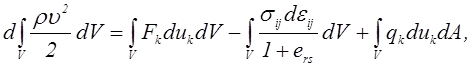
           (5.1)

Принимая во внимание, что , а 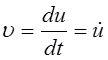 получим для левой части уравнения (5.1) следующее выражение

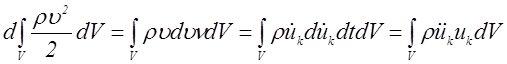
Преобразуем также второй объёмный интеграл правой части уравнения (5.1). С этой целью рассмотрим сумму  воспользовавшись формулой (2.9):

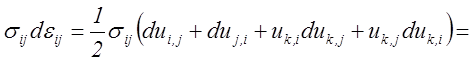
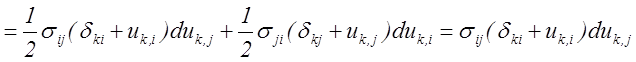
В результате рассматриваемый объёмный интеграл может быть преобразован следующим образом:

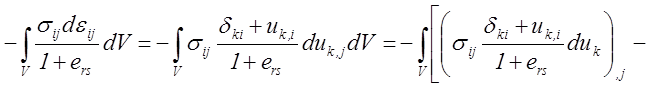
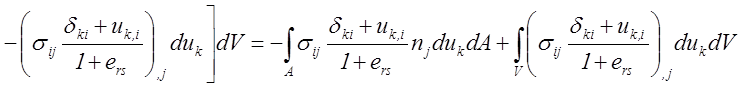
Здесь была использована формула Остроградского – Гаусса сведения объёмного интеграла к поверхностному.

Подставив преобразованные объёмные интегралы в уравнение баланса механической энергии, получим

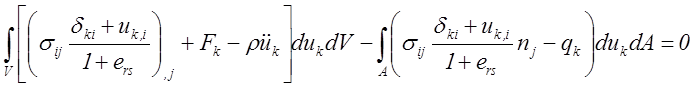
Вследствие задания при постановке задачи уравнения движения (3.45) объёмный интеграл полученного выражения тождественно равен нулю и уравнение баланса механической энергии сводится к равенству:

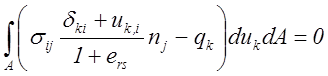                                 (5.2)

В силу линейной независимости бесконечных приращений , равенство (5.2) выполняется в двух случаях: когда равны множители при бесконечно малых приращениях перемещений , либо когда равны нулю приращения . Условия выполнения равенства (5.2) позволяют получить искомые краевые условия:

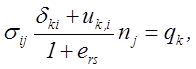
   ,                                  (5.3)

      ,                                         (5.4)

где А₁ – часть поверхности деформированного тела, свободная от закрепления в направлении координаты x_к; А₂ – часть поверхности деформированного тела, к точкам которой приложены внешние связи, недопускающие произвольного перемещения в направлении координаты x_к; u_к⁰ – заданные внешними связями перемещения точек краевой поверхности деформируемого тела.

В очень важном для практических приложениях случае малых деформаций, когда е_rs<<1 силовые краевые условия (5.3) принимают вид: