Постановка задач механики деформируемого твердого тела и схемы их решения. Условия связности многосвязного тела, страница 11

5.4. Схемы решения задач теории пластичности

Общая постановка задач механики деформируемого твердого тела приведена в п. 5.1.7. Применительно к задачам теории пластичности производится конкретизация уравнений состояния (5.19): для теории течения – это уравнения (4.68), для теории малых упруго-пластических деформаций – уравнения (4.69).

Решение упруго-пластических задач, как правило, сопряжено с огромными трудностями. Многие из них до сих пор не имеют решения. Поэтому в теории пластичности еще в большей мере, чем в теории упругости, имеют значения приближенные методы решения. Наиболее распространенными являются вариационные методы, а также методы, в которых упруго-пластическая задача сводится к последовательности упругих задач в результате применения процесса последовательных приближений. Последние методы называются методами упругих решений.

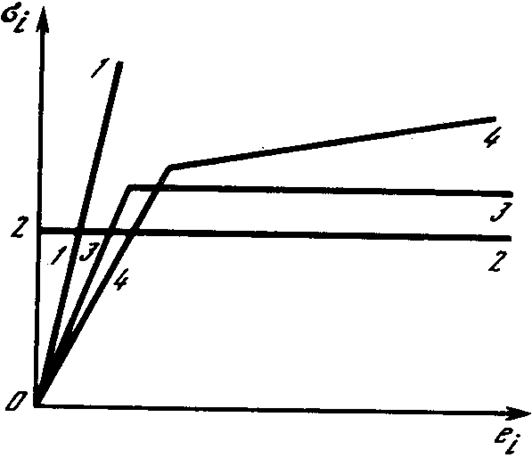
Для упрощения расчетов за пределами упругости производится схематизация реальных диаграмм деформирования, при которой реальная кривая заменяется прямыми или кривыми линиями, имеющими достаточно простое математическое описание и в тоже время достаточно близко совпадающими с реальной диаграммой. На рис. 28 показаны простейшие схематизированные диаграммы деформирования для линейно-упругого (1), жестко-пластического (2), упруго-пластического (3) и упруго-пластического упрочняющегося (4) тел.

Рис. 28. Схематизированные диаграммы деформирования.

Рассмотрим схему метода упругих решений применительно к теории течения изотропного тела.

Пусть имеется тело произвольного очертания, которое загружено объемными  и поверхностными   силами. Известен путь нагружения тела вплоть до конечных значений внешних сил. Задача состоит в определении компонентов тензора напряжений и перемещений при упруго-пластической деформации.

Разобьем весь путь нагружения на N приращений нагрузки. Если предположить, что компоненты пластической деформации для первых r приращений нагрузки известны, то значение полной деформации в конце r+1 -го приращения нагрузки определится из выражения, см. (4.29)

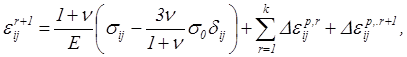                         (5.50)

где на основании (4.68)

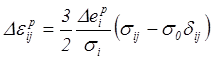.                                           (5.51)

Здесь интенсивность напряжений  определяется формулой (3.33), а интенсивность приращения пластической деформации  в случае принебрежения объёмной деформацией на основании (2.76) равна

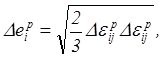                                               (5.52)

При учете температурного воздействия в выражение (5.52) добавляется еще одно слагаемое , см. (4.35).

На первой ступени нагружения  задается какой-то произвольный закон распределения приращений пластических деформаций  по объему тела, который вносится в уравнения (5.50). Тогда эти уравнения совместно с остальными составят полную систему, описывающую упругую задачу с начальными деформациями, равными , в результате решения которой находятся в первом приближении компоненты тензоров напряжений  и деформаций   на первой ступени нагружения.

С помощью формулы (5.52) на основе предварительно принятого закона распределения  по объему тела определяются интенсивности приращения пластических деформаций . По формуле

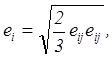
                                          (5.53)

на основе решения упругой задачи определяются интенсивности деформаций , с помощью которой по кривой , см. рис. 29, находятся . По значениям   и  из формулы (5.51) определяются уточненные величины приращения пластических деформаций .

При найденных уточненных значениях  вновь решается упругая задача и определяются уточненные значения напряжений  и деформаций . Далее повторяется вся вышеописанная процедура с предварительно принятым законом распределения  по объему тела, в результате которой производится очередное уточнение приращений пластических деформаций. Этот процесс последовательного уточнения значений   продолжается до тех пор, пока разница в значениях двух последовательных приближений для  не будет меньше некоторой допустимой величины.