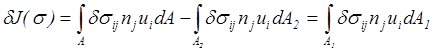Постановка задач механики деформируемого твердого тела и схемы их решения. Условия связности многосвязного тела, страница 8

.

Последний интеграл на основании второго условия (5.37) равен нулю.  Таким образом, имеем

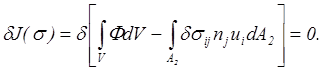
Введя обозначения

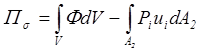,     ,                               (5.38)

где  называется полной дополнительной работой или энергией. В итоге принцип Кастильяно выражается формулой

.                                                         (5.39)

Проследив за выводом формулы (5.39), полученный результат можно сформулировать так: истинные напряжения в упругом теле реализуются только в случае полного удовлетворения уравнений движения (равновесия) и геометрии перемещения сплошного тела. Только при этих условиях функционал Кастильяно принимает стационарное значение.

Отметим, что для статических задач теории упругости точки стационарности функционалов Лагранжа и Кастильяно дают своим функционалам минимальные значения. Стационарная точка функционала Рейсснера является точкой седловатости: она доставляет максимум функционалу J(u, σ) по функциям σ_ij и минимум по функциям u_i.

В заключение отметим, что вариационный принцип Рейсснера и принципы, построенные на его основе, обладают большей общностью, чем принцип Ху-Вашицу. Последний допускает решение лишь линейных и физически нелинейных задач теории упругости, тогда как принципы типа Рейсснера никаких ограничений в теории упругости не имеют.

5.3. Основные задачи теории упругости и схемы их решения

5.3.1. Основные задачи теории упругости

Приведем полную систему линейной теории упругости в условиях статики для однородного тела:

-  уравнения равновесия, см. (3.54)

                                                (5.40)

-  уравнения геометрии перемещения сплошной среды, см. (2.54)

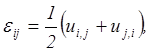                                            (5.41)

-  закон Гука для анизотропного тела, см. (4.20)

                                                 (5.42)

Система уравнений (5.40)-(5.42) решается при следующих краевых условиях, см. (5.6), (5.4)

                                                (5.43)

                                                 (5.44)

Для решения задач теории упругости предложено большое количество различных математических методов. Тем не менее многие задачи теории упругости в точной постановке до сих пор остаются практически не разрешимыми. Математические методы теории упругости эффективны при вполне определенных частных постановках задачи. Среди всевозможных постановок задач теории упругости выделяют три так называемые, основные задачи теории упругости. Первая основная задача состоит в решении системы уравнений (5.40)-(5.42) в случае, когда на всей поверхности тела задана внешняя нагрузка, т.е. при краевых условиях (5.43), распространенных на всю поверхность тела А: А₁ =А. Вторая основная задача решается в случае, когда на всей поверхности тела А заданы перемещения, т.е. при краевых условиях (5.44), распространенных на всю поверхность А: А₂: А. Наконец, рассматривается основная смешанная задача теории упругости, которая решается при краевых условиях (5.43) и (5.44). Кроме этих трех основных задач ставятся и другие более детализированные задачи теории упругости.

Отметим, что все задачи теории упругости имеют решение.

5.3.2. Единственность решения линейных задач теории упругости

В линейной теории упругости весьма важным является вопрос о том, будет ли найденное решение единственным. Заметим, что для геометрически нелинейной теории упругости этот вопрос не ставится, поскольку здесь при одних и тех же условиях внешнего воздействия на тело возможно существование нескольких форм равновесия.

Приведем доказательство теоремы единственности решения линейных задач теории упругости для линейного закона упругости (5.42).

Предположим, что при одинаковых краевых условиях одним и тем же объемным силам соответствуют два различных, решения , ,  и , , . Тогда разность этих решений    должна полностью удовлетворять всем уравнениям равновесия (5.40) при  уравнениям (5.41) и (5.42) и нулевым краевым условиям:

      .                              (5.45)