Часто бывает удобно иметь дело с уравнениями, содержащими только компоненты тензора напряжений. Одних уравнений равновесия (5/40) для этого недостаточно, т.к. три уравнения (5.40) содержат шесть неизвестных. Поэтому требуются еще дополнительные уравнения. Последние обычно находятся из условий сплошности тела (2.66), (2.67). Однако имеется более простой способ вывода уравнений теории упругости в напряжениях с использованием уравнений Ламе (5.48) [12].
Полагая, что объёмные силы равны нулю, перепишем уравнения (5.48) в виде
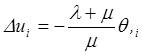
и вычислим оператор Лапласа от компонентов тензора деформаций (5.41)
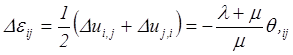
С другой стороны из уравнений закона Гука (4.28) имеем
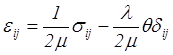
и
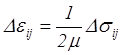, так как при 
см.
п. 5.3.3.
Приравняв между собой два различных выражения 
, получим
Воспользовавшись формулой (4.28), приведем последние уравнения к виду
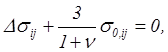(5.49)
где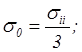 
–
коэффициент Пуассона.
Уравнения (5.49) были выведены в 1892 г. Бельтрами из условий сплошности тела и носят его имя. Уравнения с учетом объемных сил выведены Мичеллом и называются уравнениями Мичелла.
Нетрудно видеть, что
при пренебрежении объемными силами компоненты шарового тензора напряжений 
являются гармонической
функцией, а компоненты 
представляют собой бигармонические
функции. Для этого достаточно просуммировать уравнения (5.49) при j = i
(произвести
свертывание по индексу i), что дает 
, а затем взять оператор
Лапласа от (5.49): 
Система уравнений Бельтрами (5.49) имеет общий 12 порядок, который получился в результате операций дифференцирования при выводе этих уравнений. Последние операции привели к искусственному повышению порядка исходной системы. В результате оказывается, что возможные решения системы (5.49) порождают класс функций более широкий, чем возможные решения задач теории упругости. Вследствие этого решения системы уравнений (5.49) не всегда удовлетворяют уравнениям равновесия (5.40).
Система уравнений (5.49) используется для решения первой основной задачи теории упругости, т.е. в случае, когда на всей краевой поверхности задана внешняя нагрузка. При задании перемещений сформулировать краевые условия в напряженных в общем виде не удается. В результате решения системы (5.49) находятся все компоненты тензора напряжений. Затем из уравнений закона Гука определяются компоненты тензора деформаций. Для вычисления компонентов перемещений привлекаются уравнения Коши (5.41). Произвольные функции интегрирования уравнений Коши определяют перемещения и вращения тела, как жесткого целого, и находятся из условий покоя или движения жесткого тела.
Решения систем уравнений теории упругости в смешанной форме (5.40)-(5.42), в перемещениях (5.48) и в напряжениях (5.49) представляют огромные затруднения. Так называемые общие методы дают только теоретическое решение, т.е. в конечном счёте только доказывают его существование. Для получения фактических результатов используется разнообразный математический аппарат, включающий в себя классические методы и новейшие достижения последних лет. Широкое применение находят методы с применением электронно-вычислительных машин.
Не смотря на большие достижения в области вычислительной математики и техники, их современный уровень развития еще не достаточен для того, чтобы удовлетворить практические запросы в решении задач теории упругости. Поэтому широкое применение наряду с математическими методами находят различного рода упрощения, основанные на физических представлениях, которые приводят к понижению размерности задач теории упругости. Так, например, тела, у которых один размер существенно меньше двух других (пластины и оболочки) существенно в меньшей степени сопротивляются относительным перемещениям в направлении наименьшего размера (толщины), чем в двух других. Это обстоятельство позволяет ввести определенные допущения о характере работы материала в составе такого тела и тем самым свести трехмерную задачу теории упругости к двумерной. Решение же двумерной задачи на много проще трехмерной: её трудоёмкость уменьшается на три порядка, т.е. в 1000 раз.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.