Постановка задач механики деформируемого твердого тела и схемы их решения. Условия связности многосвязного тела, страница 12

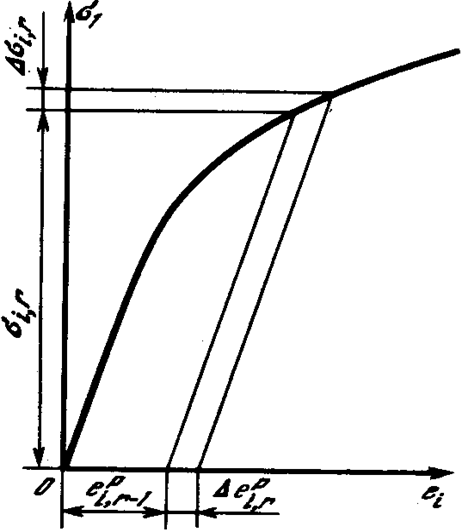
Далее рассматривается вторая ступень нагружения . Последовательность расчетов, изложенная для первой ступени нагружения полностью повторяется. Но в этом случае в формуле (5.50) появляется дополнительное слагаемое, которое определяет приращение пластических деформаций на первой ступени нагружения, т.е. формула (5.50) используется с предпоследним членом.

Рис. 29 Схема определения интенсивности напряжений.

Последовательными догружениями удается определить полную историю изменения напряженно-деформированного состояния тела в процессе всего пути нагружения.

Для обеспечения сходимости процесса последовательного приближения приращения пластических деформаций на каждом шагу не должны, как свидетельствуют числовые эксперименты, превышать величины 0,001. При сложном нагружении возможно появление в теле зон разгрузки, где следует использовать закон Гука. Для выявления зон разгрузки используются критерии, приведенные в п. 4.4.4.

При использовании теории малых упруго-пластических деформаций расчет, как правило, производится для одной ступени нагружения, куда входит вся приложенная к телу нагрузка. При этом вместо (5.50)-(5.52) используются соответственно следующие зависимости

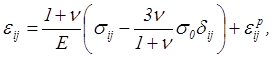                                   (5.54)

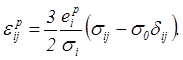                                            (5.55)

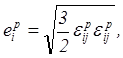                                                (5.56)

Последовательность и содержание всех вычислительных операций здесь полностью такая же, как и в предыдущем случае. Сначала задаются некоторые значения , по всему объему тела. Тогда уравнения (5.54) совместно с остальными уравнениями опишут упругую задачу с остаточными деформациями . Решение упругой задачи позволяет получить первое приближение для компонентов тензоров напряжений  и деформаций . Внося найденные значения  в формулу (5.53), находим интенсивности деформаций , с помощью которых по кривой  рис. 29, находятся интенсивности напряжений . По формуле (5.56) и предварительно заданным значениям  находятся интенсивности пластических деформаций , после чего привлекается формула (5.55), из которой определяются уточненные значения пластических деформаций . Далее уточненные значения  подставляются в формулу (5.54) и процедура полностью повторяется. Такие итерации производятся до тех пор пока разница между двумя последовательными значениями окажется несущественной.

Более подробно с современными методами решения задач пластичности можно ознакомиться в книге [23] .

5.5. Схемы решения задач теории ползучести

Полная система уравнений теории ползучести находится из общей системы уравнений механики деформируемого твердого тела (5.17)-(5.19) путем конкретизации уравнений состояния (5.19) применительно к соответствующей технической теории. При использовании теории течения уравнения (5.19) принимают вид (4.78), теории старения - вид (4.79), теории упрочнения - вид (4.81). Однозначное решение полной системы уравнений теории ползучести производится при краевых (5.20), (5.21) и начальных (5.22) условиях. Применительно к многосвязным и неоднородным телам используются дополнительные условия (5.23), (5.24) и (5.25).

При решении задач теории ползучести весь процесс деформирования разбивается на ряд временных отрезков , внутри каждого из которых можно пренебречь изменяемостью свойств материала. Эти свойства для каждого интервала времени определяются из уравнений состояния рассматриваемой технической теории ползучести. При таком подходе в пределах каждого интервала времени может быть использованы решения задач пластичности: в случае применения теорий течения и упрочнения - теория пластического течения, в случае применения теории старения - теория малых упруго-пластических деформаций.

5.6. Схемы решения задач наследственной теории ползучести

Полная система уравнений наследственной теории ползучести (вязкоупругости) включает в себя те же уравнения, что и теория упругости. Отличие заключается только в том, что в уравнениях состояния вместо упругих постоянных применены временные интегральные операторы. Решение полной системы уравнений наследственной теории ползучести производится при краевых и начальных условиях.