Понятие об управлении и системах управления. Информация и принципы управления. Цели системы управления и качества процессов достижения цели, страница 9

2.4  Структурированные модели систем управления.

Если система достаточно сложна и не поддаётся моделированию в целом, то используется приём декомпозиции – система делится на части направленного действия, которые связывают между собой линиями со стрелками.

Рассмотрим составные части некоторой системы и проведём их компоновку:

 

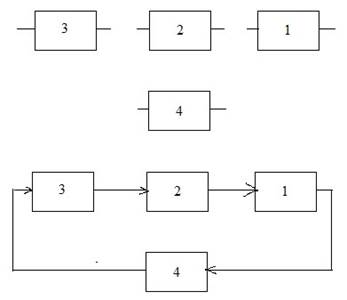
Рис. 2.4. Компоновка элементов системы.

На рисунке изображёна диаграмма графа элементов системы , где  - множество вершин;  – множество дуг.

Пусть дуги будут сигналами, а вершины – преобразователями сигналов, тогда будет получен сигнальный граф.

Следующим шагом после декомпозиции является описание моделей элементов подсистем, если они достаточно просты. Если подсистема слишком сложна для описания в целом, то она разбивается на части и т.д. Так получаются иерархические (многоуровневые) модели. Модели частей могут быть типа «вход-выход» или «вход-состояние-выход». Кроме того, элементы системы могут быть заданны частотными или временными характеристиками.

3  Анализ систем управления.

Анализ систем управления заключается в выявлении свойств устойчивости, управляемости, наблюдаемости, а также инвариантности к возмущениям, ковариантости (совместного изменения) с заданием, а также чувствительности к вариациям элементов.

3.1  Условие устойчивости.

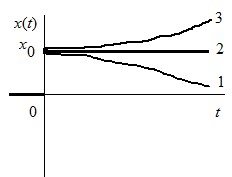
Устойчивость означает возвращение системой к прежнему состоянию после исчезновения возмущения.

 

 отражает предысторию возмущений

1  – устойчивая система

2  – граница устойчивости

3  - неустойчивая система

Решение однородного линейного дифференциального уравнения имеет вид

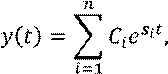
где  – различные корни характеристического полинома;  – постоянные интегрирования, зависящие от корней характеристического полинома и начальных условий Рассмотрим «моду» :

•    

•  .   Процесс       считается

установившимся, когда . Это достигается за время .

Величина  называется постоянной времени. Явления, которые описываются линейным дифференциальным уравнением с такими корнями – устойчивые.

•  .    Явления,       которые описываются линейным дифференциальным уравнением с такими корнями – неустойчивые.

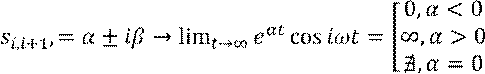•  .    При        

процесс устойчивый, при  - неустойчивый, при  процесс есть незатухающие колебания.

Вывод (необходимое и достаточное условие асимптотической устойчивости линейных стационарных систем): если все корни характеристического полинома находятся слева от мнимой оси (корни принадлежат открытой левой полуплоскости) комплексной плоскости, то система является устойчивой.

 система устойчива

3.2  Критерий устойчивости Гурвица.

Пусть дан характеристический полином линейного дифференциального уравнения:

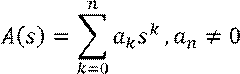
Необходимое        условие       устойчивости       системы:     все коэффициенты характеристического полинома линейного дифференциального уравнения должны быть одного знака. Обратное утверждение верно не всегда, но для дифференциальных уравнений первого и второго порядков верно и обратное утверждение.

Критерий Гурвица устойчивости систем: для устойчивости необходимо и достаточно, чтобы все диагональные миноры матрицы Гурвица были положительные.

Матрица Гурвица имеет вид:

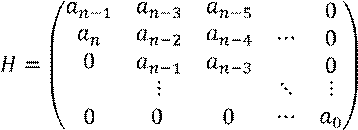
Диагональные миноры матрицы Гурвица имеют вид:

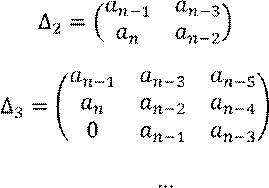
 Пример: пусть .

Составляем матрицу Гурвица:

 

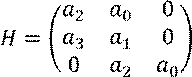
 система устойчива

Таким образом, для устойчивости произведение средних коэффициентов () должно быть больше произведения крайних коэффициентов ().  

3.3  Критерий устойчивости Михайлова.

Пусть дан характеристический полином линейного дифференциального уравнения:

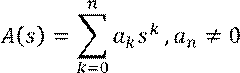
Рассмотрим  как функцию комплексного аргумента.

Пусть . Тогда, в силу основной теоремы алгебры можно разложить полином на линейные множители:

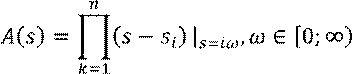
При   

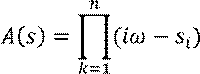
Если , и корень устойчив.

Если , и корень неустойчив.

Если все корни устойчивы, то