Понятие об управлении и системах управления. Информация и принципы управления. Цели системы управления и качества процессов достижения цели, страница 7

Частотные характеристики – зависимость параметров установившихся реакций на гармонические сигналы различных частот.

Пусть на вход подан гармонический сигнал , где , f – частота колебаний, T – период колебаний.

Реакции на гармонические сигналы линейных моделей гармонические той же формы и частоты, но, возможно, с другой начальной фазой и амплитудой.

Таблица 2.1. Значения частотных характеристик.

характеристики	1	2	4	8	16	32
Входная амплитуда
Расстояние между u и y , секунд
Разность фаз       , радиан
Усиление
, децибелл

где  - амплитудно-частотная характеристика;  - логарифмическая амплитудно-частотная характеристика;  – фазовочастотная характеристика

Резонансный пик – локальный максимум функции .

АФХ – амплитудно-фазовая характеристика (строится на комплексной плоскости: амплитуда – длина вектора, фаза -  угол между вектором и положительным направлением вещественной оси)

2.2  Построение временных характеристик.

Дифференциальные уравнения описывают динамику генератора или преобразования.

Пусть генератор генерирует сигнал  при некоторых начальных условий. Такая система описывается однородными дифференциальными уравнениями. Пусть порядок этого уравнения равен трём:

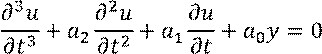
Добавим начальные условия  (начальная координата, начальная скорость и начальное ускорение).

2.2.1  Классический метод решения линейных дифференциальных уравнений.

Обозначим решение уравнения 

как . Решение ищется в форме , где s – известно. Подставим это выражение в исходное уравнение вместо y и продифференцируем:

С учётом, что  получаем

Получили характеристическое уравнение третьей степени, которое имеет три корня . Следовательно, исходное ДУ имеет решение вида

, где  определяются при помощи начальных условий из системы вида:

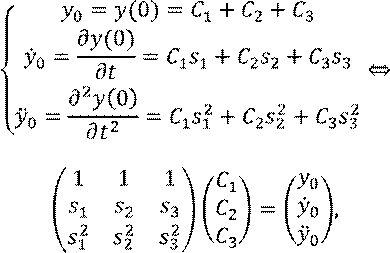
где  – матрица Вандермонда; 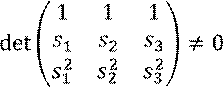 – условие существования решения;  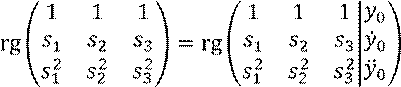– условие единственности решения

Оказывается, что формула  годится только для различных .

Таким образом, решение дифференциальных уравнений сводится к двум алгебраическим процедурам: поиск корней полиномов и решение линейных уравнений.

2.2.2  Операторный метод решения линейных дифференциальных уравнений.

               Другой    способ    решения    линейных    дифференциальных        уравнений использует преобразование Лапласа:

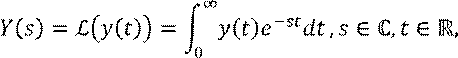
где  - оператор Лапласа.

Для применения преобразования Лапласа для решения линейных дифференциальных уравнений используется теорема о дифференцировании оригинала:

Пусть , тогда 

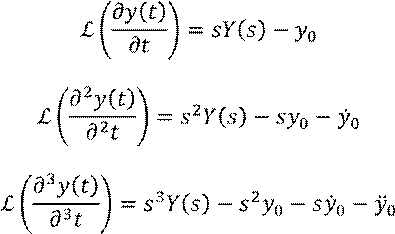
Применим к исходному уравнению оператор Лапласа:

 

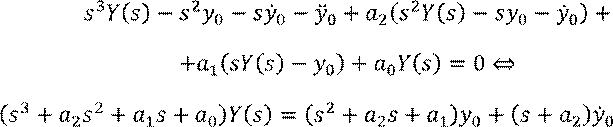
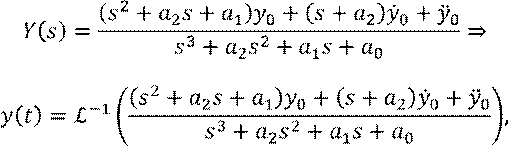
где  – дробно-рациональная функция, которую можно разложить в сумму простейших дробей.

Пусть  – простые корни , тогда  можно

представить в виде

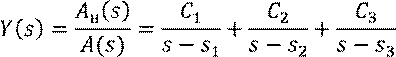
Согласно Хевисайду, при простых  имеем:

Достоинствами преобразования Лапласа

1.  При решении дифференциального уравнения сразу учитываются начальные условия.

2.  Легко решаются неоднородные дифференциальные уравнения.

2.2.3  Особенности решения неоднородных дифференциальных уравнений.

Пусть задано линейное неоднородное дифференциальное уравнение:

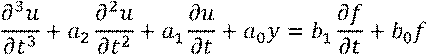
При предначальных условиях .

Решение неоднородных дифференциальных уравнений состоит из двух частей – собственной  (решение соответствующего однородного уравнения) и вынужденной  (частное решения неоднородного уравнения), т.е.