![]()
Качество процессов
характеризуют параметры ![]() и
и ![]() ,
называемые прямыми показателями качества. Хорошими считаются значения
,
называемые прямыми показателями качества. Хорошими считаются значения ![]() ,
, ![]() для
каждого процесса свое.
для
каждого процесса свое.
Доминирующие корни – корни, наименее отдалённые от мнимой оси.
Чем дальше корень расположен от мнимой оси, тем быстрее затухает переходный процесс.
Степень быстродействия (устойчивости) вычисляются по формуле:
![]()
Если корни
комплексно-сопряжённые (![]() ), то от
), то от ![]() зависит
частота затухающих колебаний.
зависит
частота затухающих колебаний.
Колебательность кореней вычисляются по формуле:
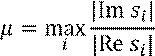
Таким образом, косвенные показатели качества – параметры ![]() и
и ![]() .
.
Хорошим считается показатель ![]() .
.
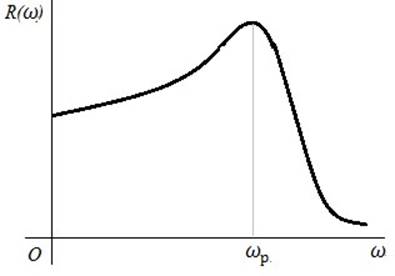
Рис. 3.4. Типовая АЧХ.
В «хорошей» системе при постоянном сигнале АЧХ должна равна 1.
Показатель колебательности вычисляется по формуле
![]()
где ![]() - частота резонанса.
- частота резонанса.
Чем больше ![]() ,
тем больше широкополосность системы и тем быстрее затухает переходный процесс.
,
тем больше широкополосность системы и тем быстрее затухает переходный процесс.
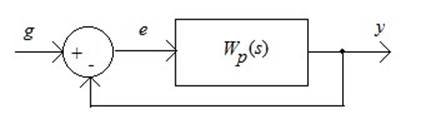
где ![]() –
передаточная функция разомкнутой системы,
–
передаточная функция разомкнутой системы, ![]()
![]() – АФХ.
– АФХ.
![]() (dcgain – усиление по
постоянному сигналу)
(dcgain – усиление по
постоянному сигналу)
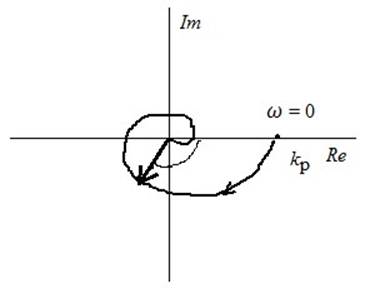
Рис. 3.5. АФХ разомкнутой системы.
Критерий Найкниста: Пусть разомкнутая система устойчива, тогда, чтобы при замыкании система не потеряла устойчивости надо, чтобы АФХ разомкнутой системы не охватывала точку (-1; 0) комплексной плоскости.
Граница
устойчивости замкнутой системы – годограф ![]()
![]() , проходящий через точку (-1;
0) комплексной плоскости.
, проходящий через точку (-1;
0) комплексной плоскости.
Желательно, чтобы система имела запас устойчивости.
![]() .
.
![]() , где
, где ![]() - частота
среза.
- частота
среза.
Запас устойчивости по амплитуде вычисляется по формуле:
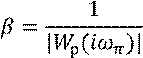
Рекомендуемые значения ![]() – от 2 до
10.
– от 2 до
10.
Запас устойчивости по фазе вычисляется по формуле:
![]()
Рекомендуемые значения ![]() - от 30°
до 60°.
- от 30°
до 60°.
Граница устойчивости достигается при ![]() .
.
При этом частота среза ![]() характеризует полосу
пропускания частот разомкнутой системы.
характеризует полосу
пропускания частот разомкнутой системы.
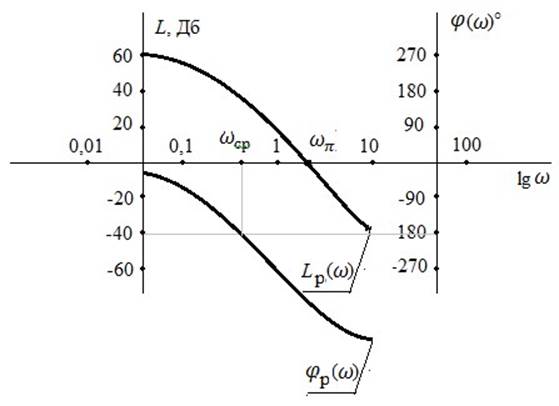
При движении к границе устойчивости ![]() сдвигается вверх Запас
устойчивости по модулю вычисляется по формуле:
сдвигается вверх Запас
устойчивости по модулю вычисляется по формуле:
![]()
![]() может быть от 6 до 20 Дб.
может быть от 6 до 20 Дб.
|
Прямые |
Косвенные |
|||
|
Корневые |
ЧХ ЗС |
ЧХ РС |
||
|
Абсолютное затухание |
|
|
|
|
|
Относительное затухание |
|
|
(показатель колебательности) |
|
В широкополосных системах переходные процессы быстро затухают.
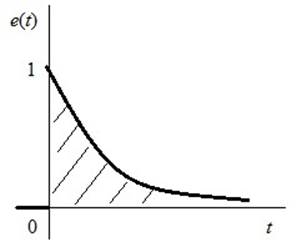
Линейный интегральный показатель качества вычисляется по формуле:
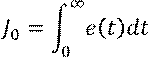
Ошибка вычисляется по формуле:
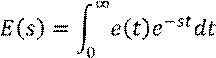
![]() , т.е. в выражении для
изображения ошибки аргумент положим равным 0.
, т.е. в выражении для
изображения ошибки аргумент положим равным 0.
Передаточная функция
замкнутой системы ![]() от задающего воздействия до
переменной ошибки e есть:
от задающего воздействия до
переменной ошибки e есть:
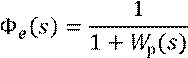
При
единичном ступенчатом воздействии изображение ошибки ![]() есть:
есть:
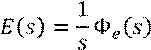
![]() Задана передаточная
функция разомкнутой системы
Задана передаточная
функция разомкнутой системы ![]() .
.
Передаточная функция замкнутой системы ![]() есть
есть
![]() .
.
С учётом, что ![]()
Имеем ![]()
![]()
С ростом k процесс становится колебательным.
Недостаток критерия в том, что он применим только к процессам, сохраняющим знак.
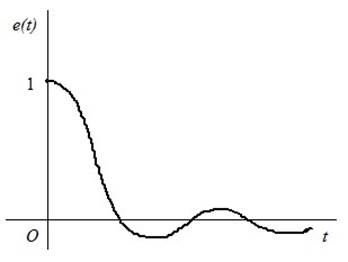
Интегральный квадратичный показатель вычисляется по формуле:
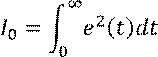
Интегральный квадратичный показатель есть норма функционального (Гильбертого) пространства.
Критерий записывается в виде
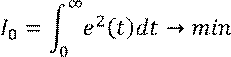
Идеальный процесс компенсации имеет вид
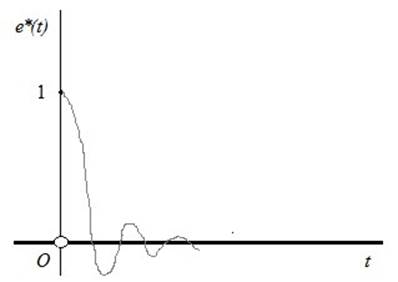
Однако, следует учитывать инерциальность.
Как вычислить ![]() не зная
не зная ![]() ?
?
Перейдём в частотную область:
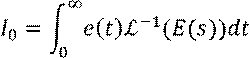
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.