Понятие об управлении и системах управления. Информация и принципы управления. Цели системы управления и качества процессов достижения цели, страница 14

Заданы дифференциального уравнения в операторной форме.

Передаточная функция регулятора:

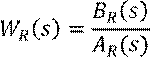
Дифференциальные уравнения для этой ПФ:

 

(«-» в силу отрицательной обратной связи)

Имеем неизвестных. Они определяют структуру регулятора.

Пусть   

Операторный метод заключается в обеспечении тождественности операторного полинома замкнутой системы заданному желаемому полиному.

Пусть характеристический полином замкнутой системы  – желаемый полином.

Известно, что:

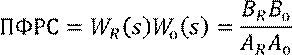
Основное уравнение операторного метода (является Диофантовым):

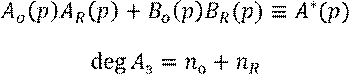
Число коэффициентов равно числу неизвестных, т.е.

Формируем :

1.  Зададимся собственными значениями .

2.  Запишем полином в виде

Из равенства полиномов получаем систему уравнений для искомых коэффициентов регулятора.

Задан СУ - перевёрнутый маятник.

 

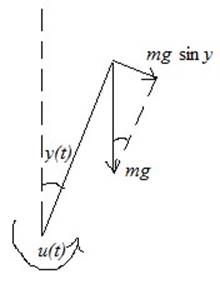
Пусть , тогда

(для малых отклонений)

ХП: .

Верхнее положение маятника неустойчиво, поэтому требуется решить задачу стабилизации.

 

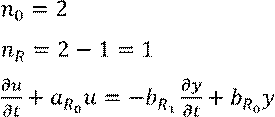
В операторной форме

 

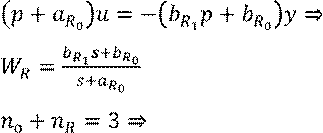
Назначим следующие корни: .

Составим основное уравнение

 

4.2.2  Метод пространства состояний.

Автономный объект задаётся уравнением

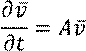
Анализируем собственные значения матрицы A.

Управляемый объект задаётся уравнением

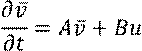
Введём регулятор состояния  и исключим переменную u:

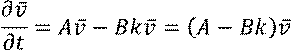
Получили автономную систему.

Здесь желаемой матрицей является матрица .

Выберем собственные значения  и сформируем характеристический полином матрицы:

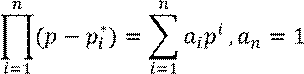
Найдём сопровождающую матрицу

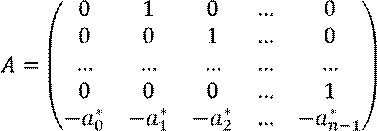
Дифференциальные уравнения объекта управления заданы в управляемой канонической форме

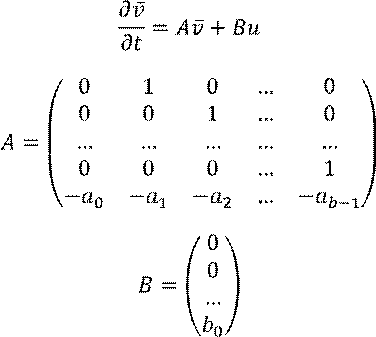
Требуется найти

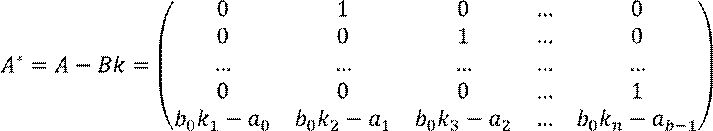
Получаем систему

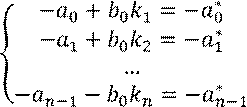
Решение которой имеет вид:

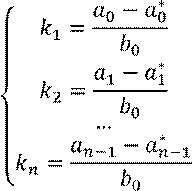
 ОУ – маятник

 

  

Перепишем это уравнение в форме пространства состояний

 

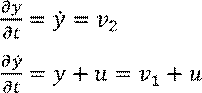
Получили:

 

Анализ устойчивости: ХП: . Система неустойчива.

Регулятор состояния .

ХП регулятора состояния:  

 

4.2.3  Наблюдатель состояния.

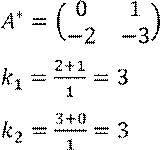
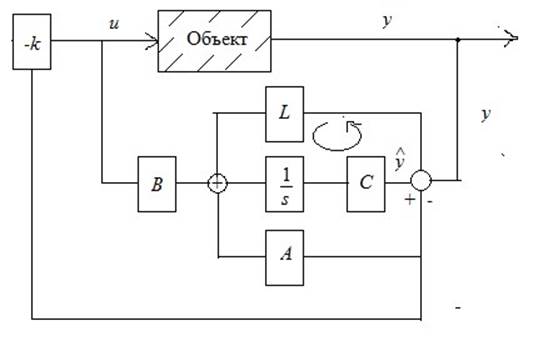
Регулятор состояния требует информации о всех переменных состояния.

Практически число измеренных переменных меньше порядка модели объекта. Для оценки непосредственно неизменяемых переменных состояния используются т.н. наблюдатели. 

Наблюдатель – вычислительное устройство, построенное по принципу обратной связи, позволяющее асимптотически отслеживать состояние объекта с использованием априорной информации о модели объекта.

Пусть дан объект управления:

 

5  СИСТЕМЫ ЦИФРОВОО УПРАВЛЕНИЯ.

5.1  Принципиальная схема системы цифрового управления непрерывным объектом.

 

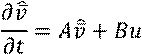
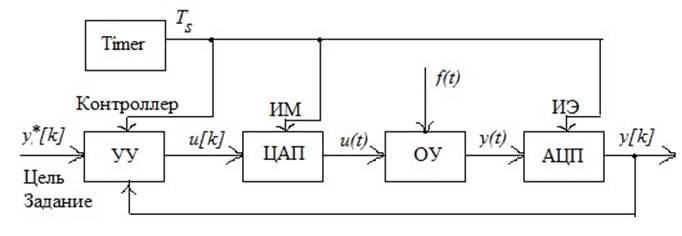
Рисунок 5.1. Концептуальная схема расширенного объекта управления.

5.2  Математическая модель расширенного объекта управления.

5.2.1  Математическая модель объекта управления.

ОУ описывается дифференциальными уравнениями, передаточными функциями или дифференциальными уравнениями в форме пространства состояний.

5.2.2  Математическая модель аналогово-цифрового преобразователя.

Если пренебречь эффектом квантовая уровней сигналов (достаточно большая разрядная сетка), то  можно рассматривать как импульсный сигнал, моделируемый в виде числовой последовательности. Тогда АЦП представляет собой «ключ»:

 

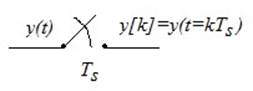
зависит от природы процесса.

5.2.3  Математическая модель цифро-аналогового преобразователя.

 

 

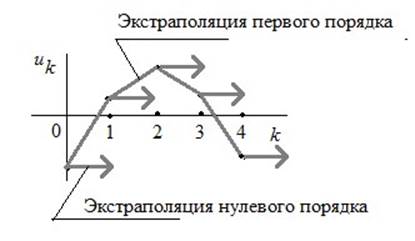
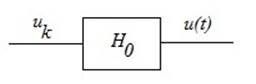
Рисунок 5.2. Обозначение ЦАП

5.2.4  Математическая модель управляющего устройства.

 

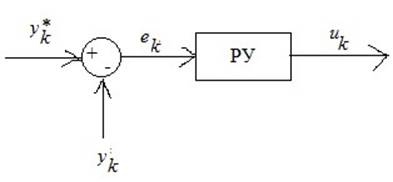
УУ описывается разностными уравнениями, дискретными передаточными функциями или разностными уравнениями в форме пространства состояний.

5.2.5  Математическая модель расширенного объекта управления.

 

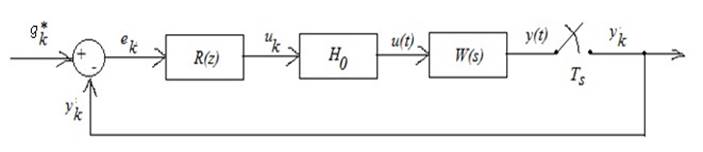
Модель получилась гибридной: непрерывная и дискретная части взаимодействуют посредством интерфейса (ЦАП  и ключ).

5.3  Разностные уравнения.

5.3.1  Понятие разностей.

Пусть дана числовая последовательность (временной ряд)

..      Чтобы         количественно     оценить       изменение значений последовательности, вводят понятие разности.