Критерий Михайлова устойчивости систем: Для устойчивости необходимо и достаточно, чтобы годограф Михайлова, начинаясь на действительной положительной полуоси, проходил последовательно n квандратнов (не пропуская) комплексной полуплоскости по часовой стрелке.
Рассмотрим два звена с передаточными функциями ![]() :
:
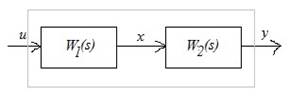
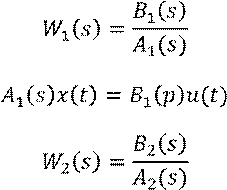
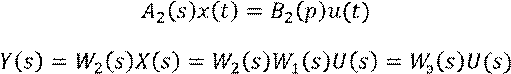
Характеристический полином системы, образованный последовательным соединением звеньев, равен произведению характеристических полиномов звеньев.
Устойчивость системы определяется устойчивостью её звеньев.
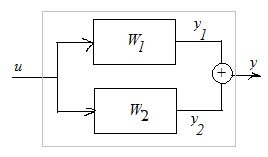
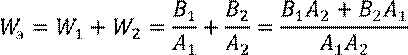
Для системы без контуров, т.е. образованной только последовательными и параллельными соединениями звеньев характеристический полином равен произведению характеристических полиномов звеньев.
Устойчивость безконтурных систем определяется только устойчивостью её звеньев.
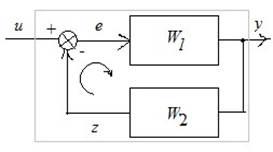
![]()
![]()
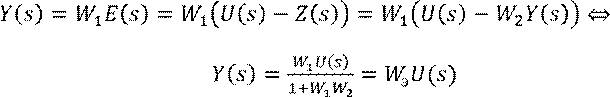
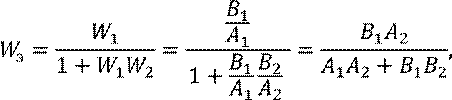
где ![]() – характеристический полином
замкнутой системы
– характеристический полином
замкнутой системы
(ХПЗС).
Рассмотрим функцию комплексного аргумента ![]() ,
где
,
где
![]() - передаточная функция
разомкнутой системы.
- передаточная функция
разомкнутой системы.
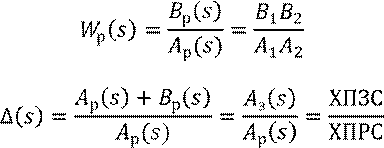
Мнемоническое правило: ХПЗС = ЧПФРС + ЗПФРС
Пусть разомкнутая система устойчивая, т.е ![]() согласно
согласно
критерию Михайлова
Для того, чтобы замкнутая система была устойчивой, требуется
![]() .
.
Следовательно, имеем критерий Найквиста:
![]()
Это
означает, что годограф ![]() не охватывает начало
координат.
не охватывает начало
координат.
Поскольку
![]() , где
, где ![]() – АФХ
разомкнутой системы, то необходимым и достаточным условием
замкнутой системы является следующее: АФХ разомкнутой системы не должна
охватывать точку с координатами (-1; 0) на комплексной плоскости. Такая система
при замыкании устойчивость не потеряет
– АФХ
разомкнутой системы, то необходимым и достаточным условием
замкнутой системы является следующее: АФХ разомкнутой системы не должна
охватывать точку с координатами (-1; 0) на комплексной плоскости. Такая система
при замыкании устойчивость не потеряет
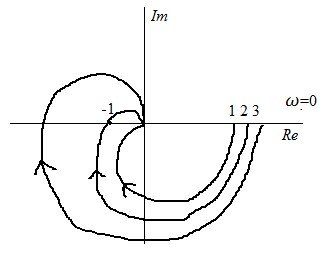
где 1 – устойчивая система; 2 – граница устойчивости; 3 – переход корней через границу
Если годограф АФХ разомкнутой системы охватывает критическую точку (-1; 0) по часовой стрелке один раз, то два корня характеристического полинома при замыкании контура перейдут в правую полуплоскость.
Если годограф АФХ разомкнутой системы охватывает критическую точку (-1; 0) против часовой стрелки один раз, то два корня характеристического полинома при замыкании контура перейдут в левую полуплоскость.
Этапы определения устойчивости систем с произвольной структурой:
1. Проанализировать устойчивость звеньев.
2. Получить характеристический полином и передаточную функцию системы. Для этого можно воспользоваться эквивалентными преобразованиями системы.
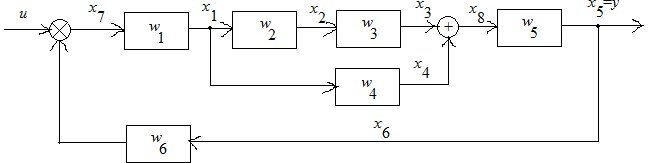
![]() Пример: найти передаточную
функцию системы
Пример: найти передаточную
функцию системы
![]()
![]()
![]() Решение:
Решение:
Используем эквивалентные преобразования:
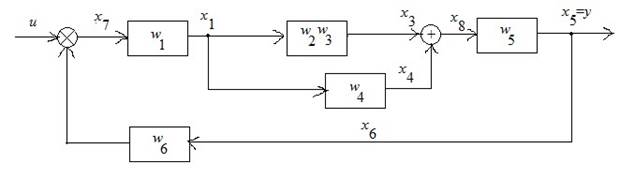
Исключили ![]() .
.
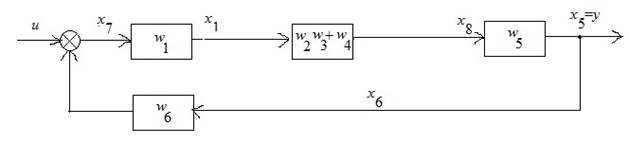
Исключили ![]()
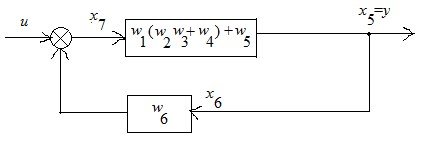
Получили систему с отрицательной обратной связью, передаточная функция которой равна:
![]()
![]() - характеристический полином
системы
- характеристический полином
системы
Ответ: ![]() .
.
Сигнальный граф – одна из возможных форм представления систем произвольной структуры.
Задаётся
множество переменных ![]() . Зададим на
. Зададим на ![]()
бинарное отношение ![]() . Если
. Если ![]() отвечают
сигналы,
отвечают
сигналы, ![]() – оператор, где
– оператор, где ![]() - следствие и
- следствие и ![]() –
причина, то
–
причина, то ![]() - сигнальный граф.
- сигнальный граф.
![]() Пусть
Пусть
![]() ,
,
![]()
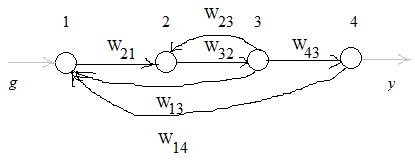
Если операторы ![]() – линейны, а в вершинах
происходит суммирование сигналов заходящих дуг, то такой сигнальный граф
называется линейным.
– линейны, а в вершинах
происходит суммирование сигналов заходящих дуг, то такой сигнальный граф
называется линейным.
Пусть необходимо получить передаточную функцию между двумя вершинами сигнального графа.
Рассмотрим изображения переменных по Лапласу и, соответственно, передаточную функцию дуг.
![]() Рассмотрим граф
Рассмотрим граф

и запишем по нему уравнения:
![]() (линейное уравнение в
причинно-следственной
(линейное уравнение в
причинно-следственной
![]()
![]()
![]()
![]() форме: слева – следствие, справа - причины)
форме: слева – следствие, справа - причины)
Запишем эти уравнения в матричной форме:
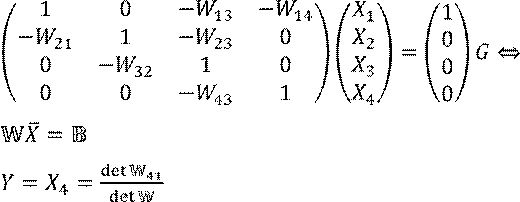
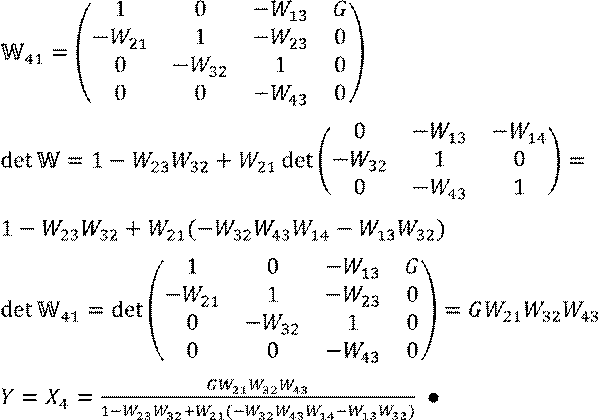
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.