Формула Мэйсона является топологическим аналогом правила Крамера.
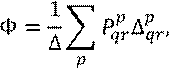
где ![]() -
определитель сигнального графа;
-
определитель сигнального графа; ![]() - передаточная функция пути от
вершины r до вершины q;
- передаточная функция пути от
вершины r до вершины q; ![]() - минор p-го
пути, равный определителю подграфа, полученного удалением p-го пути
- минор p-го
пути, равный определителю подграфа, полученного удалением p-го пути
![]()
где ![]() – передаточная функция k-го
контура;
– передаточная функция k-го
контура; ![]() – произведение передаточных функций пар непересекающихся
контуров;
– произведение передаточных функций пар непересекающихся
контуров; ![]() - произведение передаточных
функций троек непересекающихся контуров В формуле использованы следующие
топологические понятия:
- произведение передаточных
функций троек непересекающихся контуров В формуле использованы следующие
топологические понятия:
1. Путь – последовательность вершин и дуг, в которой каждый элемент встречается ровно один раз.
2. Контур – замкнутый путь, т.е. путь, последняя вершина которого совпадает с первой.
3. Отношения касания: если контуры имеют общие вершины, то говорят, что они касаются друг друга.
![]()
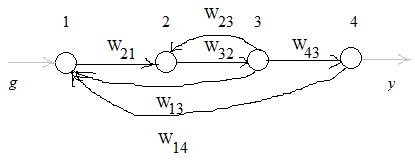
![]()
![]()
![]() Контуры:
Контуры:
![]()
![]()
![]() Все
контуры соприкасаются друг с другом.
Все
контуры соприкасаются друг с другом.
Пути:
![]()
Получили ![]() .
.
![]()
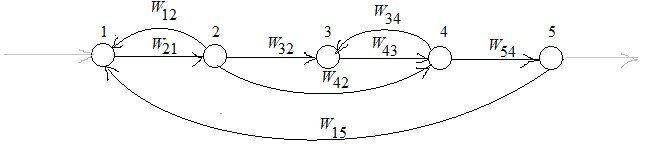
![]()
![]()
![]() Контуры:
Контуры:
Пара не касающихся контуров - ![]() .
.
![]()
![]()
![]() Пути:
Пути:
Миноры
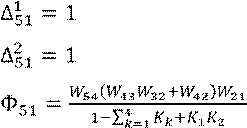
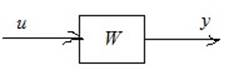
Рис. 3.1. Схема LTI.
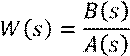
Требуется представить данную систему в виде совокупности простых.
Переход к совокупности простых систем неоднозначно.
Дифференциальные уравнения записываются в виде:
![]()
где ![]() .
.
Требуется привести эту систему к форме пространства состояний:
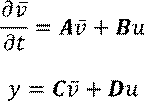
![]() записать как дифференциальное
уравнение.
записать как дифференциальное
уравнение.
![]()
Проблема состоит в выборе переменных состояния (компонент ![]() ).
).
Возьмём т.н. «естественный базис»: ![]()
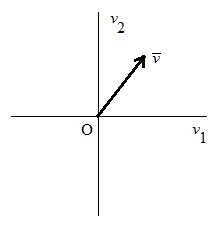
Рис. 3.2. Геометрическое представление переменных состояния.
Неоднозначность возникает при выборе базиса.
Получаем:
![]()
![]()
![]()
![]()
Или, в матричной форме:
![]()
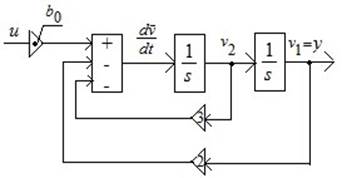
Рис. 3.3. Схема модели в форме пространства состояний.
Таким образом, для реализации требуются интеграторы, сумматор и усилители.
Рассмотрим уравнение n-го порядка:
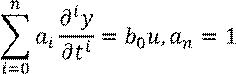
Разрешим это уравнение относительно старшей производной:
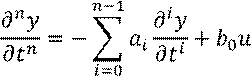
Записываем переменные состояния в «естественном базисе»:
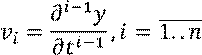
Записываем исходное уравнение в форме пространства состояний
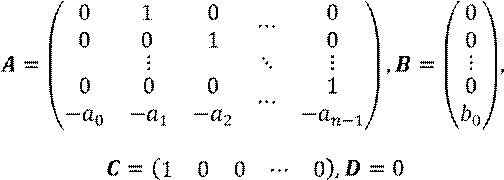
Матрица A еще называется сопровождающей матрицей или матрицей Фробениуса.
Пусть задана передаточная функция:
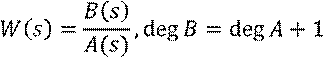
Разделим ![]() на
на ![]() с
остатком:
с
остатком:
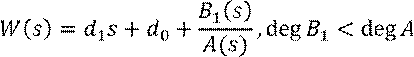
Пусть корни ![]() уравнения
уравнения ![]() (полюсы
(полюсы
![]() ) – простые.
) – простые.
Тогда
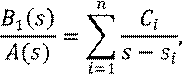
где ![]() (формула Хевисайда)
(формула Хевисайда)
Получили следующую реализацию:
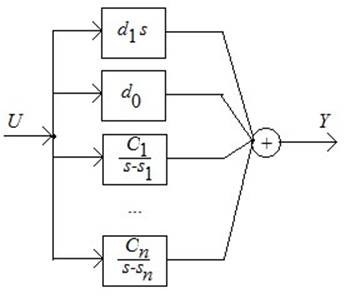
Таким образом, для
реализации требуется дифференциатор, усилители, для звеньев с ![]() -
интегратор, для звеньев с
-
интегратор, для звеньев с ![]() - устойчивое звено первого
порядка с коэффициентом усиления
- устойчивое звено первого
порядка с коэффициентом усиления ![]() и постоянной времени
и постоянной времени ![]()
![]()
![]()
![]() , для звеньев с комплексно
сопряжёнными корнями
, для звеньев с комплексно
сопряжёнными корнями ![]() - звено второго порядка
- звено второго порядка ![]() , где
, где ![]() -
коэффициент демпфирования. При
-
коэффициент демпфирования. При ![]() звено будет апериодическим и
звено будет апериодическим и ![]() , что даёт 2 последовательно соединённых усилительных
звена, при
, что даёт 2 последовательно соединённых усилительных
звена, при ![]() комбинированное звено, при
комбинированное звено, при ![]() консервативное звено.
консервативное звено.
Пусть задана передаточная функция:
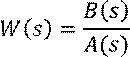
Представим ![]() в виде произведения:
в виде произведения:
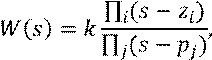
где ![]() - нули передаточной функции;
- нули передаточной функции; ![]() - полюса передаточной
функции.
- полюса передаточной
функции.

Если система устойчива, то процессы затухают. Это является необходимым условием работоспособности систем. Однако, этого не достаточно – желательно, чтобы процессы затухали достаточно быстро, без излишней колебательности.
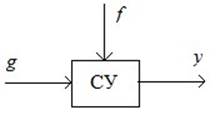
Требования к системам управления:
1. Инвариантность к возмущениям.
2. Ковариантность к заданию.
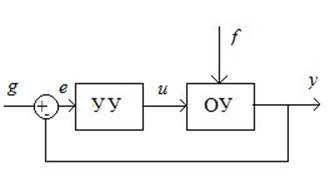
Требуется, чтобы
![]()
Пусть на вход подана ![]() . Если система «хорошая»
(принцип обратной связи реализован и правильно выбран алгоритм управления), то
. Если система «хорошая»
(принцип обратной связи реализован и правильно выбран алгоритм управления), то
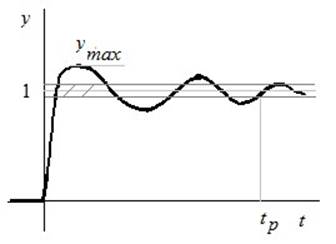
Цель - минимизировать ![]() и
и ![]() – время перерегулирования.
– время перерегулирования.
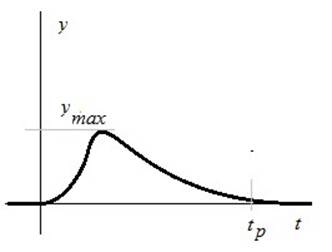
Переходный процесс при отсутствии регулирования:
Переходный процесс завершается с точностью 5%.
![]() Функция
Функция ![]() затухает
до 5% за время
затухает
до 5% за время ![]() .
.
![]()
Перерегулирование рассчитывается по формуле:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.