Понятие об управлении и системах управления. Информация и принципы управления. Цели системы управления и качества процессов достижения цели, страница 13

Используем формулу обратного преобразования Лапласа:

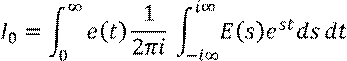
Поменяем порядок интегрирования:

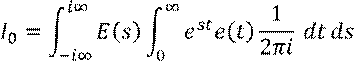
Используем формулу для :

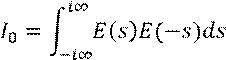
Формула Парсеваля:

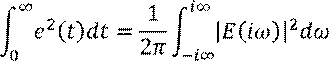
Где  – энергия процесса.

Пусть n – порядок системы.

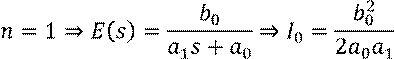
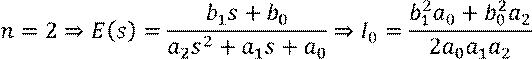
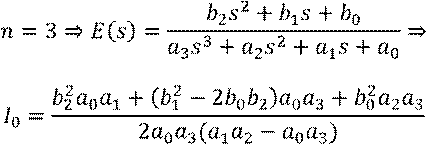
 Задана система:

 

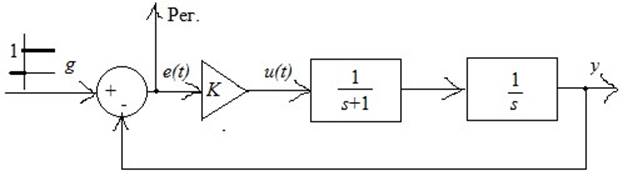
Требуется определить параметр k.

Решение:

Запишем передаточную функцию разомкнутой системы:

 

Запишем передаточную функцию замкнутой системы по ошибке:

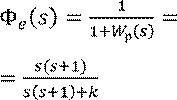
Знаменатель  есть характеристический полином замкнутой системы.

Условие устойчивости: для устойчивости системы требуется, чтобы все коэффициенты характеристического полинома замкнутой системы были положительными, поэтому  (необходимое условие устойчивости).

Для  условие  является и достаточным.

 

  

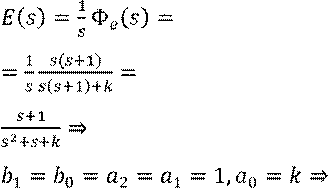
Рассмотрим корневые показатели качества.

Запишем ещё раз характеристический полином замкнутой системы и вычислим его корни:

 

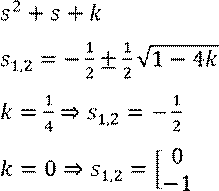
Построим годограф корней в зависимости от k:

 

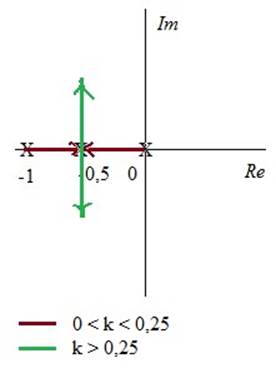
- с ростом k растёт частота.

, если огибающая  есть

Таким образом,  достаточно просто вычисляется, однако, его минимизация приводит к сильно колебательным системам, что создаёт трудности на практике.

3.7.4.3«Улучшенный» интегральный квадратичный показатель.

Из-за большой крутизны кривых сильно колебательных систем значения  больше, чем у слабо колебательных систем.

«Улучшим» интегральный квадратичный показатель:

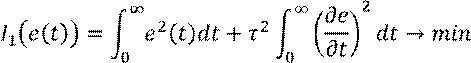
где  - весовой коэффициент.

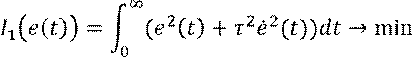
Какая функция  доставляет минимум функционалу ? Это задача вариационного исчисления.

Выделим полный квадрат в подынтеральном выражении:

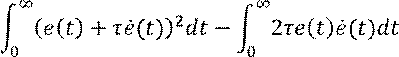
Упростим второй интеграл (с учётом , в силу устойчивости системы ):

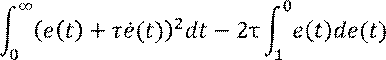
Получили:

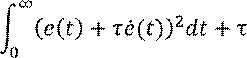
Пусть . Тогда должна быть решением уравнения

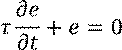
Получили

 – постоянная времени.

Таким образом, формализация требований к качеству процессов связаны с выбором постоянной времени .

3.7.4.4  Обобщённый интегральный квадратичный показатель.

Ограничим и ускорение процесса при помощи критерия ():

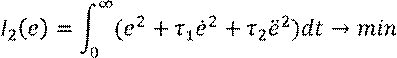
Найдём  - минимум функционала .

 – решение ДУ

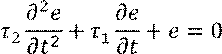
Если дифференциальное уравнение системы представлено в форме пространства состояний

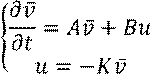
Требуется синтезировать регулятор состояния, выбрав K.

Критерий без ограничений по управлению:

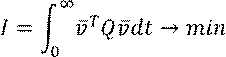
где Q – положительноопределённая матрица.

Критерий с ограничениями по управлению:

 

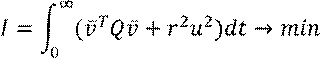
где Q – положительноопределённая матрица.

Синтез 

4  СИНТЕЗ СИСТЕМ УПРАВЛЕНИЯ.

4.1  Задача синтеза.

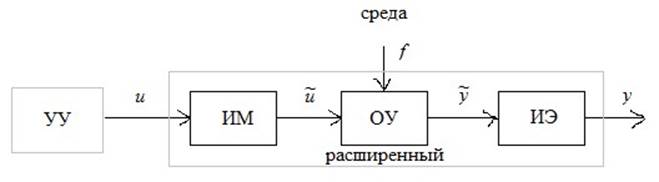
Пусть дан объект управления, находящийся под воздействием среды:

 

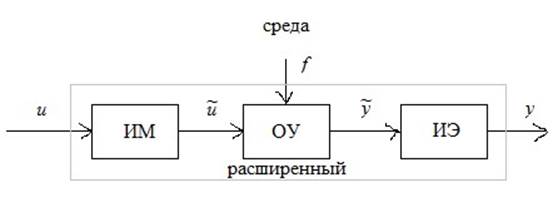
 – сигналы-носители информации, ОУ – обрабатывает информацию.

Пусть даны: 

•  Математическая модель ОУ (например, в виде дифференциальных уравнений).

•  Модель среды.

•  Требования / пожелания («модель проектировщика»).

Ограничения: 

•  Динамические свойства, характеристики ОУ.

•  Управляющие воздействия.

•  Ограничения на переменные.

4.1.1  Синтез управления.

 

Пусть задана программа . Найти , где  - множество допустимых управлений.

В статическом случае  или . Если задано , то можно найти , решив уравнение.

В динамическом случае , причём множество  ищется отдельно.

4.1.2  Стабилизация неустойчивых режимов объекта управления.

Пусть дан объект без самовыравнивания:

 

4.1.3  Подавление возмущений.

 

4.2  Стабилизация неустойчивых объектов.

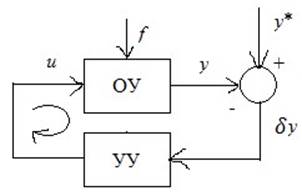
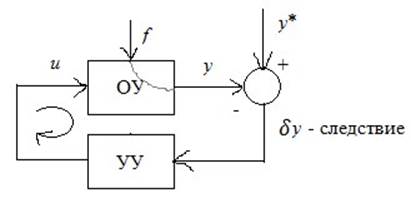
Для простоты рассмотрим линейную математическую модель. Пусть дано дифференциальное уравнение в операторной форме:

Анализ корней характеристического полинома показал, что существует неустойчивые корни или корни «левые», но с плохими показателями (например, процессы сильно колебательные). Необходимым условием изменения динамики является охват объекта обратной связью, т.е. построение замкнутой системы:

 

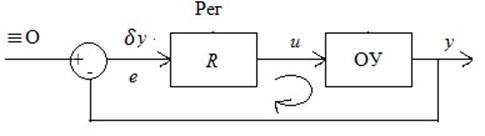
Искомое дифференциальное уравнение регулятора имеет вид:

Передаточная функция регулятора имеет вид:

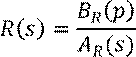
Передаточная функция разомкнутой системы:

4.2.1  Операторный метод.

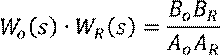
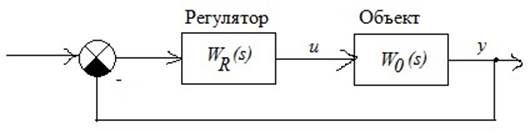
Задана система управления