Аналитический способ построения математических моделей применяется для объектов хорошо изученной природы.
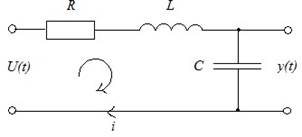
![]() RLC-цепь
RLC-цепь
![]()
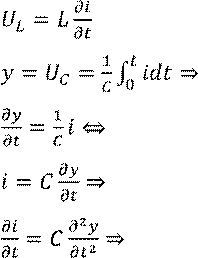
![]() (ЗНК)
(ЗНК) ![]()
![]()
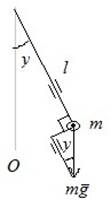
![]() Маятник
Маятник
В отличие от RLC-цепи маятник – генератор.
![]()
Выводы:
1. Объекты электрической и механической природы моделируются дифференциальными уравнениями одинакового вида.
2. Исследование механических объектов можно проводить по электрическим.
Формулы для расчёта параметров эквивалентной маятнику цепи:
• ![]()
• ![]()
• ![]()
Т.о четырёхполюсник является физической (аналоговой моделью маятника).
Рассмотрим абстрактную модель – дифференциальное уравнение второго порядка:
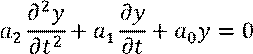
Для решения дифференциального уравнения можно соответствующим образом построить электрическую цепь, с помощью которой можно получить решение этого дифференциального уравнения, что является основой аналоговых вычислительных машин.
Задан объект в виде «черного ящика». Требуется описать этот объект математически.
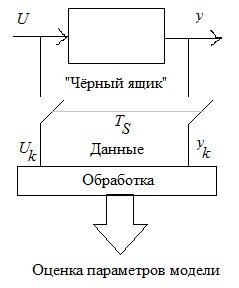
Свойства моделей:
1. Линейность.
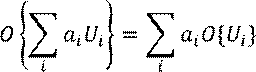
2. Стационарность – свойства оператора не зависят от времени.
3. Детерминированность – параметры модели не являются случайными величинами.
4. Конечномерность – сосредоточенность параметров.
Системный анализ включает в себя:
1. Обособление объекта
2. Перечисление переменных, связывающих объект и окружающую среду.
3. Введение упрощений и гипотез.
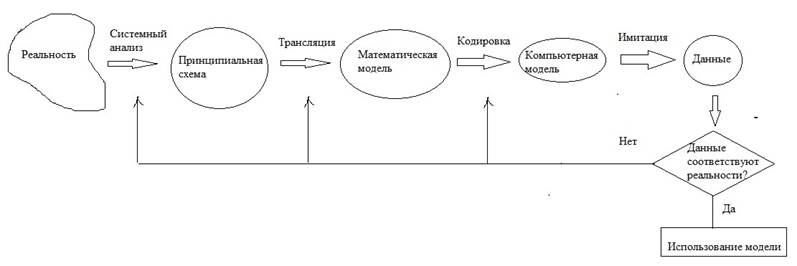
Рис. 1.12. Аналитический способ построения модели.
Если объект уже существует, тогда используется идентификация, которая начинается с работы над математической моделью.
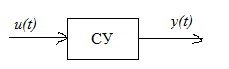
Рис. 2.1. Фильтр.
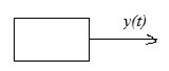
Рис. 2.2. Генератор.
Различные процессы протекают с различными скоростями. Поэтому алгебраических уравнений недостаточно для описания этих процессов.
Линейные дифференциальные уравнения первого порядка содержат скорость протекания процесса:
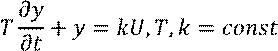
Линейные дифференциальные уравнения, разрешённые относительно производной, называются дифференциальными уравнениями в форме Коши:
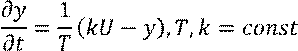
Линейные дифференциальные уравнения второго порядка содержат скорость и ускорение протекания процесса:
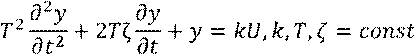
Неоднородное линейное дифференциальное уравнение есть модель фильтра.
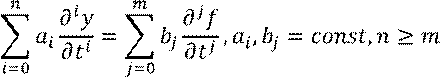
Однородное линейное дифференциальное уравнение есть модель генератора.
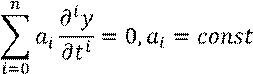
Обычно к дифференциальному уравнению добавляются начальные условия.
Перейдём к изображению выходного сигнала и входного воздействия при помощи преобразования Лапласа:
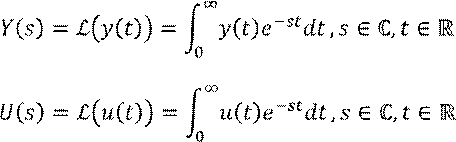
Свойство линейности преобразования Лапласа следуют из свойств интеграла:
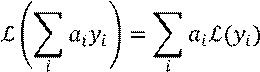
Теорема о дифференцировании оригинала
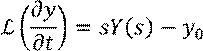
Преобразование Лапласа линейного дифференциального уравнения при нулевых начальных условиях есть алгебраическое уравнение:
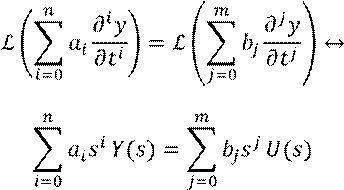
Передаточная функция – отношение изображений по Лапласу сигнала на выходе к сигналу на входе при нулевых начальных условиях.
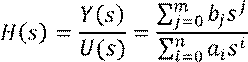
Передаточная функция есть динамический коэффициент усиления.
Передаточная функция не учитывает предысторию процесса.
По передаточной функции легко восстановить линейное дифференциальное уравнение и наоборот.
Если ![]() , то процесс является
статическим.
, то процесс является
статическим.
Если ![]() , то процесс является
динамическим.
, то процесс является
динамическим.
Временные характеристики - реакции на типовые воздействия при нулевых начальных условиях.
Типы воздействий:
1.
Единичная импульсная функция Дирака ![]()
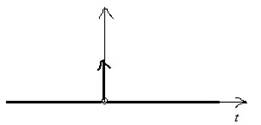
2.
Единичная ступенчатая функция Хевисайда ![]() Связь
Связь ![]() и
и ![]() :
:
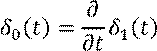
Реакция на ![]() при
нулевых начальных условиях есть импульсная функция (функция веса)
при
нулевых начальных условиях есть импульсная функция (функция веса) ![]() .
.
Реакция на ![]() при
нулевых начальных условиях есть переходная характеристика
при
нулевых начальных условиях есть переходная характеристика ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.