Понятие об управлении и системах управления. Информация и принципы управления. Цели системы управления и качества процессов достижения цели, страница 8

Используем преобразование Лапласа для решения линейного неоднородного дифференциального уравнения:

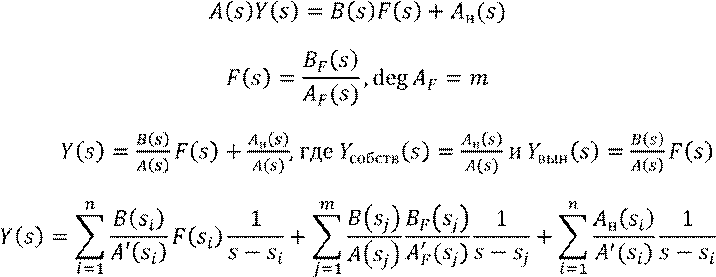
Известно, что  

 Пример 1: На вход динамической системе с коэффициентом усиления (передаточной функцией)  подан сигнал  при нулевых начальных условиях. Определить сигнал на выходе (переходную характеристику).

Решение:

 

 

 

 

 

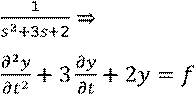
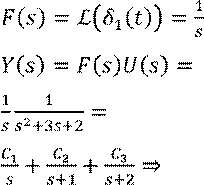
Получили сумму т.н. типовых изображений:

 

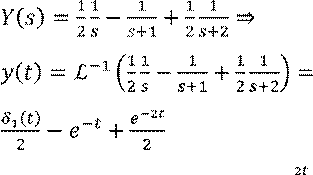
Ответ: .  

Пример 2: На вход динамической системе с коэффициентом усиления (передаточной функцией)  подан сигнал  при нулевых начальных условиях. Определить сигнал на выходе (импульсную характеристику).

Решение:

 

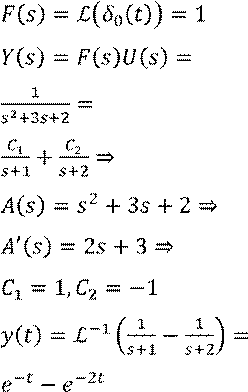
Ответ:   

Замечание: импульсная характеристика есть обратное преобразование Лапласа от передаточной функции.  

2.2.4  Построение частотных характеристик.

Частотные характеристики - зависимости амплитуды и фазы установившихся реакций от частоты при гармонических сигналах различных частот на входе.

Установившимся реакциям в системе отвечают частные решения неоднородного дифференциального уравнения.

Пусть задано дифференциальное уравнение второго порядка:

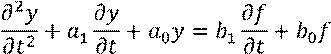
Пусть система устойчива, поэтому не интересуемся начальными условиями. В устойчивой системе переходные процессы, вызванные преднулевыми начальными условиями и посленулевыми начальными условиями из-за внезапного включения генератора сигнала , затухают.

Пусть .

Будем искать частное решение заданного уравнения в форме

.     Предполагается,    что     установившаяся                                                         реакция

линейной системы на гармонический сигнал имеет гармоническую форму и ту же частоту, что и входной сигнал. Требуется определить амплитудно-частотную характеристику  и фазочастотную характеристику .

Подставим

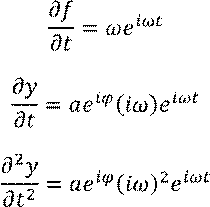
В исходное уравнение:

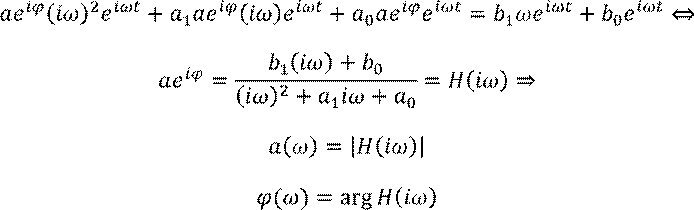
где  – передаточная функция при .

               Логарифмическая                                     АЧХ                    (ЛАЧХ)

 «растягивает» малые частоты и «сжимает» большие.

         Пример 1: Усилительное         (безинерционное) звено описывается уравнением .

(усилитель не вносит фазовых сдвигов)

 

  

 Пример 2: Интегрирующее звено

 

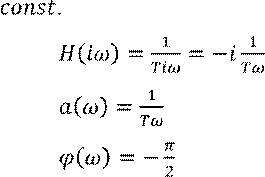
Интегратор находится на границе устойчивости.

 

В координатах   - линейная функция.

Усиление частоты в десять раз (на декаду) приводит к усилению ЛАЧХ в -20 раз.   

 Пример 3: Апериодическое звено первого порядка.

Дифференциальное уравнение апериодического звена первого порядка имеет вид:

,  где T – постоянная времени; k – коэффициент усиления

  

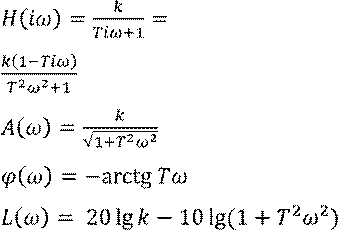
При , т.е. на низких частотах апериодическое звено первого порядка ведёт себя как усилитель с коэффициентом k.

При , т.е. на высоких частотах апериодическое звено первого порядка ведёт себя как интегратор.

2.3  Модели «вход-состояние-выход».

Пусть дан n-мерный вектор состояния .

Модели «вход-состояние-выход» записываются в виде дифференциальных уравнений:

Вход – уравнение состояния:

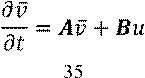
Уравнение выхода:

где ;  – матрица состояний;  – матрица входа;  - матрица выхода;  - матрица обхода.

 

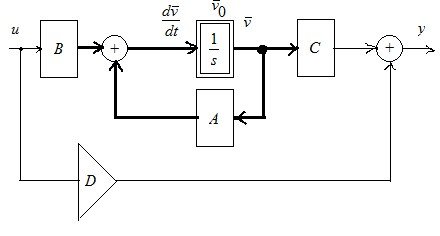
Рис. 2.3. Схема ДУ модели «вход-состояние-выход»

Графическое         представление      дифференциальных           уравнений, описывающих систему вход-состояние-выход.

Применим к дифференциальным уравнениям, описывающим систему вход-состояние-выход преобразование Лапласа при нулевых начальных условиях:

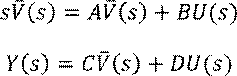
Выразим  через :

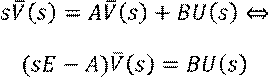
               Пусть    ,      тогда ,         где                – характеристический полином.

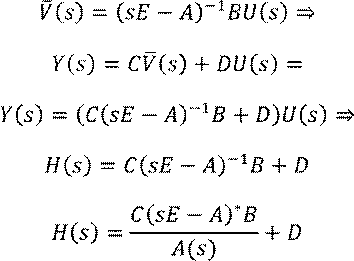
где  - передаточная функция

                     Пример:     Система     задана     следующими дифференциальными уравнениями

 

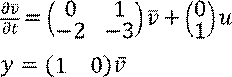
Требуется определить передаточную функцию.

Решение:

(характеристическая матрица)

 

 (характеристический полином)

Матрица  ищется с помощью двух операций: транспонирования и замены каждого элемента его алгебраическим дополнением:

 

Получили  Ответ: