Разность первого порядка есть:
![]()
Если ![]() ,
то последовательность при переходе от
,
то последовательность при переходе от ![]() к
к ![]() растёт, если
растёт, если ![]() ,
то последовательность при переходе от
,
то последовательность при переходе от ![]() к
к ![]() не изменяется, если
не изменяется, если ![]() последовательность при
переходе от
последовательность при
переходе от ![]() к
к ![]() убывает.
убывает.
Разность второго порядка есть:
![]()
Разности высших порядков строятся аналогично.
Разностные уравнения содержат последовательности и их разности различных порядков. Поскольку разности можно представить через значения последовательностей в соседних точек, то разностные уравнения обычно записывают в следующей форме:
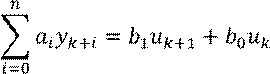
Допускается «сдвинуть» на k элементов последовательности:
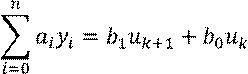
Как и в дифференциальных уравнениях, имеются начальные условия
![]() .
.
![]() Генератор чисел Фибоначчи.
Генератор чисел Фибоначчи.
Известно, что ![]() (Изначально
(Изначально ![]() -
число пар кроликов). Это разностное уравнение второго порядка.
-
число пар кроликов). Это разностное уравнение второго порядка.
Сдвинем индекс: ![]() .
.
Стандарные начальные условия ![]() ,
, ![]()
![]() - итеративное решение
разностного уравнения.
- итеративное решение
разностного уравнения.
Разностные уравнения являются готовым алгоритмом итеративного решения, если оно разрешено относительно старшего члена.
![]() Генератор
псевдослучайной последовательности.
Генератор
псевдослучайной последовательности.
Алгоритм конгруэтный (т.к. использует операцию получения остатка от деления):
![]()
где ![]()
Пусть ![]()
Справедиво соотношение
![]() , т.е последовательность
полученных чисел имеет равномерное распределение.
, т.е последовательность
полученных чисел имеет равномерное распределение.
На языке MATLAB этот генератор имеет вид:
mu = 1; lambda = 5; G(1) = 5; N = 16; for k = 1:2*N
G(k + 1) = rem(1 + 5 * G(k), N); end
![]() Фильтр МА(3).
Фильтр МА(3).
Пусть фильтр подключен к генератору псевдослучайных чисел, имеющих равномерное распределение. Требуется получить последовательность псевдослучайных чисел, имеющих нормальное распределение.
![]()
Разностные уравнения, разрешённые относительно старшего члена, являются готовым алгоритмом итерационного решения. Вместе с тем, представляет интерес выражение для произвольного члена последовательности.
Рассмотрим процедуру решения разностного уравнения на примере.
![]() Пусть
задано уравнение
Пусть
задано уравнение ![]() . Будем искать решение в форме
. Будем искать решение в форме
![]() , где k известно.
, где k известно.
Подставим ![]() в исходное уравнение:
в исходное уравнение:
![]()
С учётом, что ![]() имеем
имеем
![]()
Получили характеристическое уравнение разностного уравнения.
![]()
Линейная комбинация ![]() есть решение исходного
уравнения.
есть решение исходного
уравнения. ![]() и
и ![]() находятся
из системы:
находятся
из системы:
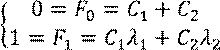
Или в матричном виде:
![]() где
где ![]() - матрица Вандермонда
- матрица Вандермонда
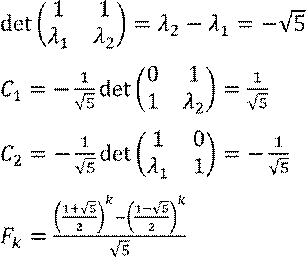
Эта формула называется формулой Бине.
Значение аналитического выражения для решения в том, что имеется возможность анализа асимптотики решения и внутренних структурных свойств последовательности.
Эмпирически
было получено, что ![]() и
и
![]() .
.
![]() Доказательство: в формуле
Бине берём
Доказательство: в формуле
Бине берём ![]()
Известно, что ![]() .
.
Следовательно,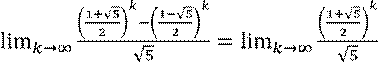
Ряд Фибоначчи растёт как экспонента.
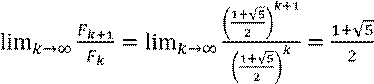
![]()
Условие устойчивости.
Общее решение разностного уравнения имеет вид
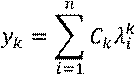
где ![]() - различные корни
характеристического полинома.
- различные корни
характеристического полинома.
Условие устойчивости (![]() ) имеет
вид:
) имеет
вид:
![]()
где ![]() - различные корни
характеристического полинома.
- различные корни
характеристического полинома.
Необходимое условие устойчивости: характеристический полином
![]() должен удовлетворять
соотношениям:
должен удовлетворять
соотношениям:
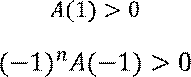
Для ![]() это условие является ещё и
достаточным.
это условие является ещё и
достаточным.
Для гибридных систем нет общих аналитических методов исследования.
Поэтому используется компьютерная имитация (например в
MATLAB/Simulink).
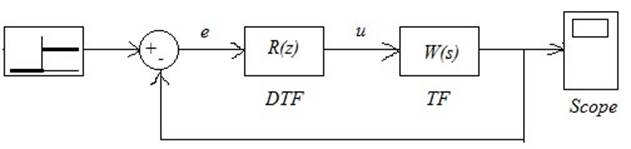
АЦП и ЦАП встроены в дискретные блоки. Нужно только задать периоды дискретизации.
Из модели управления
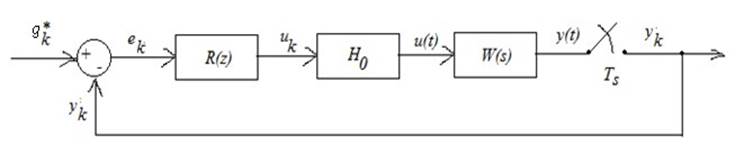
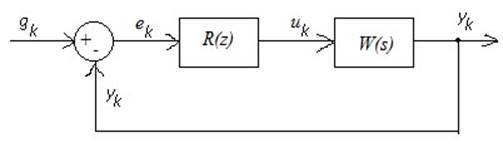
Построим однородную модель. Для этого нужно исключить либо непрерывные, либо дискретные переменные.
Однородные дискретные модели ориентированы на ЦЭВМ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.