Для регулирования этой системы используются следующие законы:
• Пропорциональный закон (П-закон):
![]()
• Интегральный закон (И-закон):
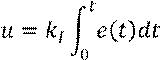
• Пропорционально-интегральный закон (ПИ-закон):
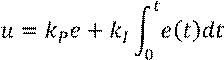
• Пропорционально-интегрально-дифференциальный закон (ПИДзакон):
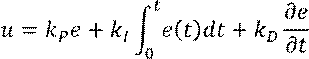
Для исполнения решений управляющего устройства необходима энергия.
Различают прямое и непрямое регулирование.
Прямое регулирование использует энергию самого объекта.
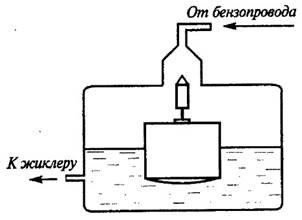
Рис. 1.8. Пример системы прямого управления (карбюратор автомобильного двигателя).
Достоинство прямого управления - простота.
Недостаток прямого управления – низкая точность из-за совмещения информационных и энергетических функций.
Непрямое регулирование использует посторонний источник энергии.
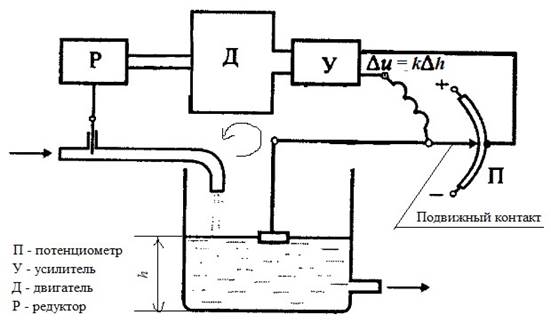
Рис. 1.9. Пример системы непрямого регулирования (система для стабилизации уровня жидкости).
Цели системы управления:
1. Стабилизация
выхода объекта управления ![]() .
.
2. Программа
изменения выхода объекта управления ![]() .
.
3. Следящие
системы управления за случайным процессом ![]() .
.
4. Экстремальные
системы управления ![]() .
.
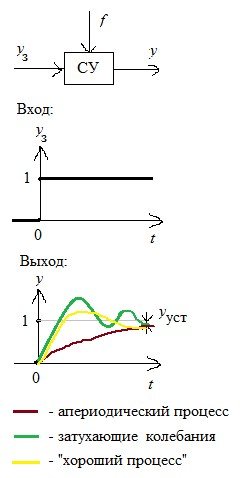
Рис. 1.10. Процессы достижения цели СУ.
Развитая теория опирается на математические модели.
Сигнал как математическая модель – переменная, зависящая от времени
![]() .
.
Виды сигналов:
•
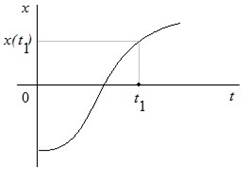
Аналоговые ![]() , время
, время ![]() -
непрерывно, в любой момент времени информация доступна.
-
непрерывно, в любой момент времени информация доступна.
•
Импульсные ![]()
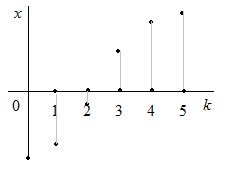
Реальное время вычисляется по формуле:
![]()
где ![]() – время выборки (период дискретизации времени).
– время выборки (период дискретизации времени).
•
Релейный ![]() , где
, где ![]() –
некоторое непустое конечное множество.
–
некоторое непустое конечное множество.
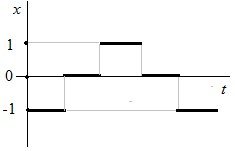
Говорят, что произведено квантование уровней сигнала.
•
Цифровой ![]() – квантован, время – дискретно.
– квантован, время – дискретно.
Таблица 1.1. Виды сигналов.
|
|
Непрерывный |
Дискретный |
|
Непрерывный |
Аналоговый |
Импульсный |
|
Квантованный |
Релейный |
Цифровой |
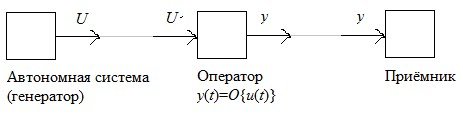
Рис. 1.11. Система управления.
Математическое описание этой системы:
1. Пусть задан аналоговый сигнал, тогда оператор представляет собой дифференциальное уравнение, которое содержит переменные и их производные по времени:

Для генератора уравнение принимает вид:
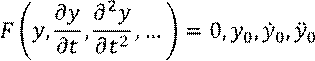
2. Пусть задан импульсный сигнал, тогда оператор представляет собой разностное уравнение второго порядка
![]()
где ![]() - разность первого порядка;
- разность первого порядка; ![]()
![]() - разность второго порядка.
- разность второго порядка.
3. Пусть задан релейный сигнал, тогда оператор – конечный асинхронный автомат.
4. Пусть задан цифровой сигнал, тогда оператор – конечный синхронный автомат (компьютер).
Таблица 1.2. Математические структуры, описывающие сигналы.
|
|
Непрерывный |
Дискретный |
|
Непрерывный |
Дифференциальные уравнения |
Разностные уравнения |
|
Квантованный |
Конечные асинхронные автоматы |
Конечные синхронные автоматы |
1. Анализ
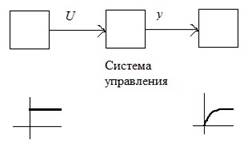
Известно U, известны параметры системы управления, но не известно y.
2. Синтез системы управления (синтез фильтра) / идентификация объектов
Известно U, известно y, но неизвестны параметры системы управления.
3. Синтез управления.
Известно y, известны параметры системы управления, но не известно U.
Теория имеет дело с математическими моделями, которые требуется построить.
Существуют два способа построения математических моделей:
• Аналитический (дедукция).
• Экспериментальный (индукция).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.