Понятие об управлении и системах управления. Информация и принципы управления. Цели системы управления и качества процессов достижения цели, страница 16

Исключим непрерывный элемент. Пусть система задана дифференциальными уравнениями в форме пространства состояний:

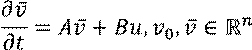
Перейдём к разностным уравнениям в форме пространства состояний:

Для этого требуется задать период дискретизации .

5.7.1.1  Метод Эйлера для одномерных систем.

Рассмотрим непрерывную систему с :

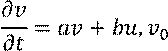
Преобразуем эти уравнения к дискретным.

По определению производной:

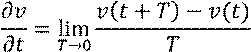
Зададим малое T. Тогда:

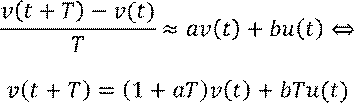
Пусть , тогда

5.7.1.2  Устойчивость при дискретизации.

Условие устойчивости для системы, заданной дифференциальными уравнениями , а для дискретизированной - .

Решением неравенства  есть , т.е. T не должно быть большим.

5.7.1.3  Метод Эйлера для многомерных систем.

Пусть система задана дифференциальными уравнениями в форме пространства состояний:

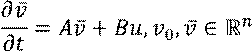
Тогда формулы метода Эйлера имеют вид:

5.7.1.4  «Точный» метод перехода к дискретной модели.

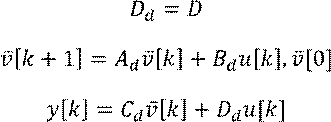
Пусть система задана дифференциальными уравнениями в форме пространства состояний:

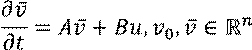
Преобразуем первое уравнение по Лапласу:

 

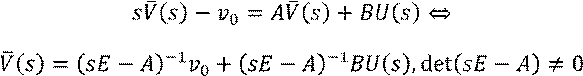
В скалярном случае

В векторном случае  (свободное движение).

Известно, что  (по теореме о свёртке)

(вынужденное движение) Окончательно имеем:

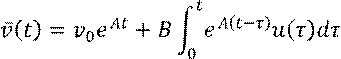
Пусть  и рассмотрим временной интервал

. Тогда , что вносит ошибку (замена непрерывной функции ступенчатой). Имеем при , :

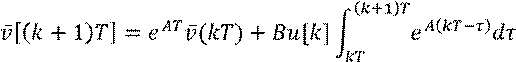
Пусть , тогда  и

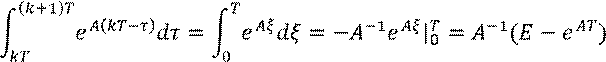
Получили формулы дискретизации

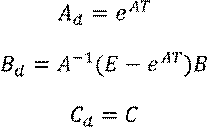
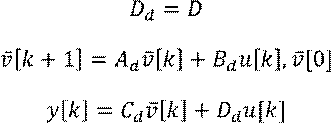
где  переходная матрица.

При преобразовании квадратных матриц по некоторой функциональной зависимости получается квадратная матрица того же размера, собственные значения которой связаны с собственными значениями исходной матрицы (аргумента) той же зависимостью: пусть  - собственные значения матрицы ,  собственные значения матрицы , тогда

.

Пусть , тогда , , т.е. из устойчивой непрерывной системы всегда получается устойчивая дискретная система.

5.7.1.5  Дискретная передаточная функция объекта управления.

Пусть заданы разностные уравнения в форме пространства состояний:

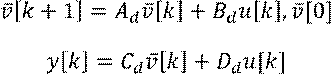
Выполним дискретное преобразование Лапласа (z-преобразование):

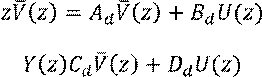
Выразим из первого уравнения  и подставим во второе:

 

5.7.2  Выбор периода / частоты дискретизации.

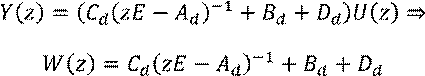
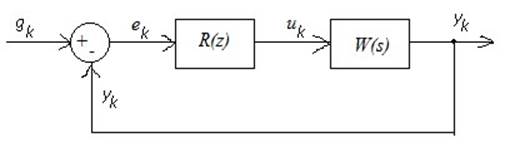
Пусть входной сигнал имеет гармоническую форму и период T (частоты

, циклической частоты ). Не менее двух раз нужно измерить сигнал за один период, чтобы определить амплитуду сигнала, т.е. .

Следовательно   , где  – частота Найкниста.

Для периодических сигналов используется разложение в ряд Фурье:

 

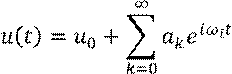
Имеет смысл ограничить число членов ряда Фурье числом N: .

Согласно теореме Котельникова-Шеннона, имеем .

Пусть входной сигнал апериодический. Для апериодических сигналов используется интеграл Фурье.

5.7.3  Однородные непрерывные модели.

Задана модель:

 

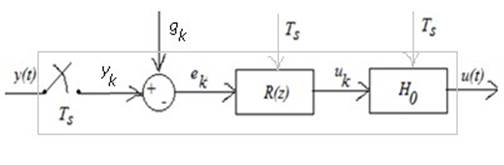
Требуется получить континуализированную (непрерывную) модель.

Формулы перехода от непрерывных моделей к дискретным:

Откуда получаем формулы для перехода от дискретных моделей к непрерывным:

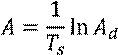
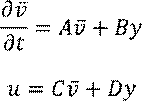
Если дискретная система первого порядка имеет отрицательное действительное собственное значение, то она не может быть преобразована к непрерывной системе первого порядка. Это связано с тем, что собственные числа матриц  и ,  и  связаны (логарифм отрицательного числа есть комплексное число), а у непрерывной системы первого порядка собственное значение не является комплексным.

Движение в дискретных системах несколько богаче, чем в непрерывных.

5.8  Дискретные системы с конечным временем затухания.

В устойчивых непрерывных системах процессы затухают, теоретически, бесконечно. Если дискретная система имеет нулевые собственные значения, то соответствующая составляющая движения затухает за один такт. Если разностные уравнения n-го порядка имеет m нулевых собственных значений, то процесс длится не более чем m тактов. 

Задано разностное уравнение в операторной форме:

где  – полином n-ой степени; q – оператор сдвига, т.е. .