Медиана – такое число, что вероятности для случайной величины оказаться меньше него и больше него одинаковы.
Мода – такое число, что вероятность для случайной величины принять это значение больше, чем для какого-либо другого числа.
Дисперсия – это мат. ожидание для случайной величины, равной квадрату отклонения значения рассматриваемой случайной величины от ее мат. ожидания. Квадратный корень из дисперсии называется среднеквадратическим отклонением.
Нетрудно заметить, что математическое ожидание, медиана, мода и среднеквадратическое отклонение являются аналогами соответствующих статистических показателей. Мат. ожидание соответствует среднему выборочному, остальные показатели называются одинаково.
И действительно, при большом количестве испытаний теоретические и статистические показатели случайной величины практически совпадают. Это говорит нам Закон больших чисел.
Согласно Закону больших чисел, случайная величина, равная среднему значению из n независимых случайных величин (с ограниченной дисперсией, т.е. все значения эти величин ограничены определенным числом, проще говоря, эти величины примерно одного масштаба), при достаточно большом n имеет мат. ожидание, которое почти не отличается от среднего мат. ожиданий этих случайных величин. Т.е., чем больше n, тем меньше вероятность такого отличия. Этот закон вполне понятен интуитивно. Допустим, если случайная величина принимает с равной вероятностью значения 1 (орел) и -1 (решка) и ее мат. ожидание, следовательно, равно 0, то вполне естественно, что при 100 испытаниях примерно 50 из них дадут 1, и столько же -1, и таким образом среднее опять будет равным 0.
Не так очевидна Центральная предельная теорема, которая говорит о том, что сумма n независимых случайных величин при достаточно большом n подчиняется нормальному закону распределения (точнее, вероятность отклонения от этого закона при росте n стремится к нулю). Центральная предельная теорема важна для практики. Многие случайные события представляют собой результат взаимодействия большого количества независимых или слабозависимых случайных событий, поэтому соответствующие случайные величины имеют распределение, близкое к нормальному.
Нормальное распределение, это такое распределение, для которого плотность распределения выражается следующей формулой:
![]()
Где μ – математическое ожидание случайной величины и δ – ее среднеквадратическое отклонение.
График плотности распределения для нормального распределения выглядит следующим образом:
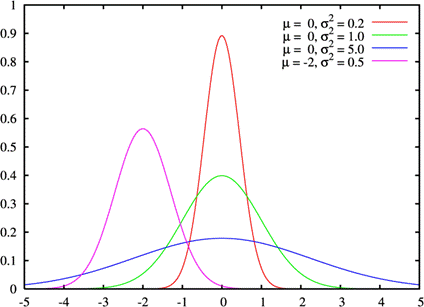
Площадь под линией графика функции распределения на каком-либо отрезке равна вероятности того, что случайная величина примет значение из этого отрезка.
Нормальное распределение с мат. ожиданием, равным 0 и среднеквадратическим отклонением, равным 1, называется стандартным нормальным распределением.
Теоретические и статистические показатели.
Таким образом, признак можно представить как случайную величину, характеризующуюся определенным математическим ожиданием и среднеквадратическим отклонением. В качестве значений теоретических показателей при статрегулировании берутся их статистические аналоги. По-хорошему, математическое ожидание (взятое как среднее выборочное) должно совпадать с нормальным значением признака, а среднеквадратическое отклонение (взятый как статистическое среднеквадратическое отклонение выборки) – с допустимым отклонением. Если это не так, то есть повод задуматься о состоянии техпроцесса. Если, например, нормальное значение плотности материала изделия после прессования равно 30, а статистическое среднее выборочное (и, следовательно, математическое ожидание) равно 35, то, скорей всего, отклонение от нормы не является полностью случайным, а имеет устойчивый, «необходимый» сдвиг (в данном случае – на 5), а уже отклонения от этого сдвинутого значения подчиняются случайному закону. Следовательно, если мы устраним фактор, который приводит к неслучайному сдвигу, то фактические значения будут колебаться уже вокруг нормативного значения и доля изделий, соответствующих норме, увеличится.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.