Социология и политология \ Социология

Анализ социологических данных с применением пакета SPSS. Пошаговая исследовательская модель анализа данных, страница 13

Таблица 1. Доля людей старше 45 лет и доля людей, негативно оценивающих будущее в районах города

Район

Доля людей 45 лет и старше

Доля людей, негативно оценивающих свое будущее

Дзержинский

0,483

0,372

Железнодорожный

0,521

0,309

Заельцовский

0,492

0,303

Калининский

0,453

0,214

Кировский

0,521

0,374

Ленинский

0,491

0,28

Октябрьский

0,444

0,241

Первомайский

0,606

0,365

Советский

0,474

0,245

Центральный

0,569

0,327

Таблица 2. Коэффициенты корреляции и детерминации

Model

R

(коэффициент корреляции)

R Square

(коэффициент детерминации)

Adjusted R Square (скорректированный коэффициент детерминации)

Std. Error of the Estimate (стандартная ошибка оценки)

Durbin-Watson (коэффициент Дурбина-Уотсона)

1

0,689(a)

0,474

0,409

0,0441

1,847

a  Predictors (независимая переменная): доля людей старше 45 лет и старше

b  Dependent Variable (зависимая переменная): доля людей, негативно оценивающих будущее

Таблица 3. Однофакторный дисперсионный анализ

Модель

Sum of Squares

(сумма квадратов)

df

Mean Square (средний квадрат)

F-статистика

Sig.

(Значимость)

Regression (модель)

0,014

1

0,014

7,221

0,028(a)

Residual (остатки)

0,016

8

0,002

-

-

ВСЕГО

0,030

9

-

-

-

Таблица 4. Коэффициенты регрессионной модели

Коэффициенты модели

Нестандартизованные коэффициенты

Unstandardized Coefficients

Стандартизованные коэффициенты

Standardized Coefficients

t

статистика

Sig.

(Значимость)

B

Std. Error

Beta

Константа

-0,093

0,148

-

-0,628

0,547

доля людей старше 45

0,783

0,291

0,689

2,987

0,028

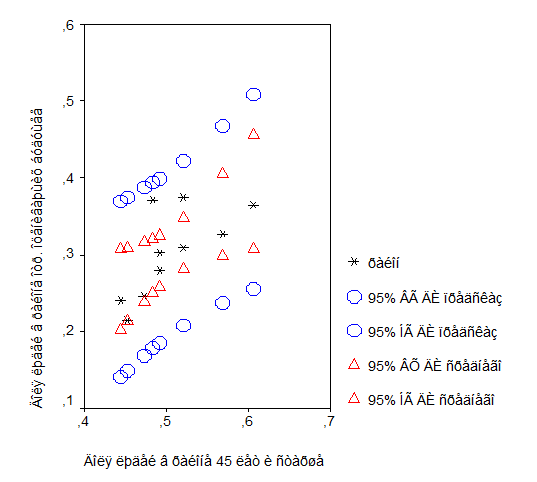
Рис.  Зависимость доли людей 45 лет и старше и доли, негативно оценивающих будущее, доверительные интервалы предсказания и среднего предсказания


Бинарная логистическая регрессия

(Процедура REGRESSION/ BINARY LOGISTIC)

Модель бинарной логистической регрессии предназначена для тех случаев, когда зависимая переменная является дихотомической. Независимые переменные могут быть измерены в любых шкалах, в том числе и быть категориальными признаками. Пример: зависимый признак – готовность доверять окружающим (обобщенное доверие); независимые признаки – две оценки локуса-контроля индивида.

Табл. 1 – 3 являются вспомогательными. В них отражены преобразования, которым подверглись исходные переменные для включения в модель. Данные табл. 4 – 7 позволяют судить о качестве модели на каждом шаге ее построения (по мере включения в модель независимых признаков), а также о конечной варианте (соотношение наблюдаемых и предсказанных событий). В табл. 8 представлены регрессионные коэффициенты. Рисунок дает наглядное представление о распределении наблюдаемых значений в соответствии с заданной точкой разрыва.

Таблица 1. Количество объектов, включенных в анализ (Case Processing Summary)

Скачать файл