Социология и политология \ Социология

Анализ социологических данных с применением пакета SPSS. Пошаговая исследовательская модель анализа данных

Страницы работы

40 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Материалы к лекциям по курсу

«Анализ социологических данных

с применением пакета SPSS»

Пошаговая исследовательская модель анализа данных

(на основе схемы, предложенной Ю. Толстовой в работе «Логика математического анализа социологических данных. М.: Наука, 1999. С. 34)

Методологические основания математико-статистических моделей имеют решающее значение для анализа социологических данных. Всегда стоит помнить, что статистические модели являются инструментом для проверки теоретических гипотез исследования. Соответственно, анализ и интерпретация данных – промежуточное звено исследовательского процесса. В представленной схеме отражена идея необходимости взаимосвязи различных этапов исследовательской работы. В рамках данного курса особое значение имеет переход от формальной модели к апостериорной содержательной модели.

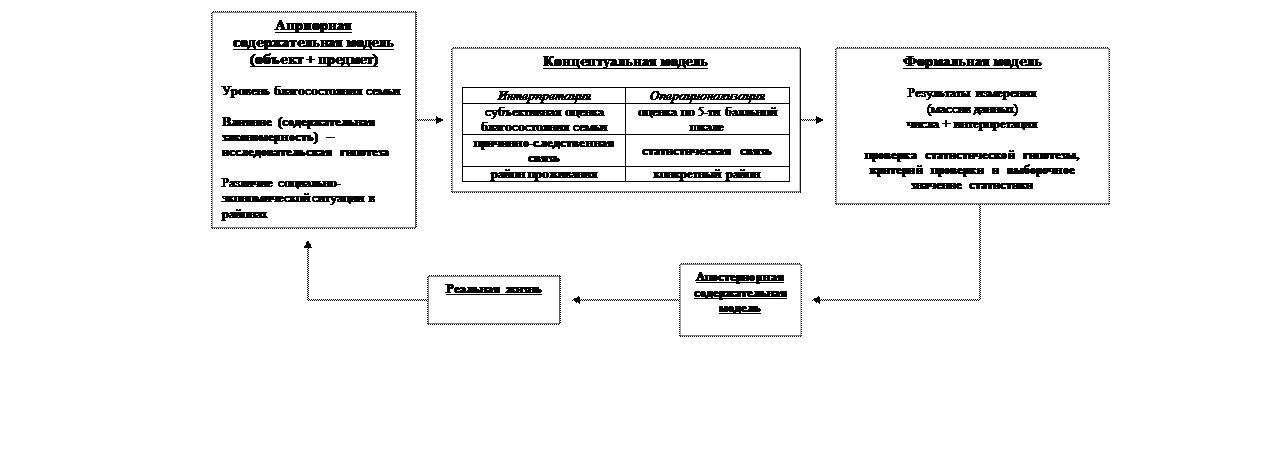
Общая схема проверки статистической гипотезы

(Источник: Малхотра Н. Маркетинговые исследования. М.: Вильямс, 2003. С.563)

На схеме представлены альтернативные способы проверки статистических гипотез. В пакете SPSS реализован первый способ (эмпирический уровень значимости соотносится с заданным критическим уровнем). Однако, воспользовавшись математико-статистическими таблицами, можно реализовать и второй способ проверки.

Одномерные частотные распределения

(Процедура FREQUENCIES)

Построение одномерных частотных распределений является первым шагом анализа количественных данных. В табл. 1 представлены возможные варианты «линеек»: количество объектов в группах, процент от опрошенных, валидный процент (процент от тех, кто ответил на вопрос), накопленный процент. В табл. 2 приведены различные статистики выборочного распределения интервального признака, которые могут быть получены с помощью процедуры Frequencies. На рис. отображено распределение данного признака с наложенной кривой нормального распределения для осуществления «глазомерного» способа проверки «нормальности» выборочного распределения.

Таблица 1. Распределение респондентов по возрастным группам

Возрастные группы	Количество (frequency)	% от опрошенных (percent)	% от ответивших (valid percent)	Накопленный процент (cumulative percent)
18 – 24	193	16,4	16,4	16,4
25 – 34	198	16,9	16,9	33,3
35 – 44	169	14,4	14,4	47,7
45 – 54	239	20,3	20,3	68,0
55 – 64	178	15,1	15,1	83,1
65+	198	16,9	16,9	100,0
Всего	1175	100,0	100,0	-

Таблица 2. Оценки параметров распределения признака «возраст»

N (количество)	Valid (валидное количество)	1175
	Missing (системные ошибки)	0
Mean (среднее)		44,75
Median (медиана)		46,00
Mode (мода)		50
Std. Error of Mean (стандартная ошибка среднего)		0,497
Std. Deviation (стандартное отклонение)		17,046
Variance (дисперсия)		290,557
Skewness (статистика скошенности)		0,081
Std. Error of Skewness (стандартная ошибка скошенности)		0,071
Kurtosis (статистика пикообразности)		-1,153
Std. Error of Kurtosis (стандартная ошибка пикообразности)		0,143
Range (размах)		64
Percentiles (процентили, 3 равные группы)	33,3	35,00
	66,7	54,00

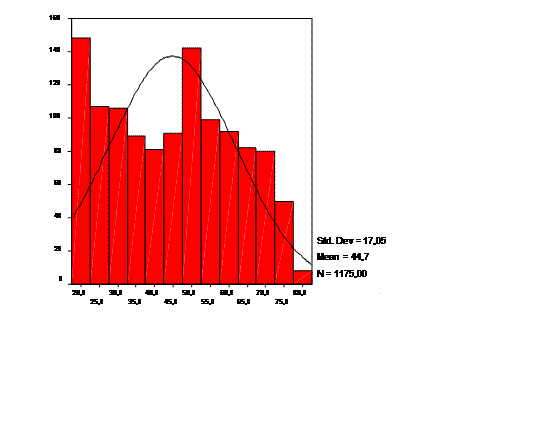
Рис.1 Гистограмма распределения возраста

Таблицы сопряженности и меры связи

(Процедура CROSSTABS)

Таблицы сопряженности являются инструментом исследования взаимосвязи двух переменных (номинальных или ранговых с небольшим количеством альтернатив). Табл. 1 содержит частотное распределение признака «оценка городской ситуации» в трех возрастных группах. В табл. 2 представлены полезные для анализа взаимосвязи отдельных альтернатив признаков Z–статистики, а также ожидаемое (в условиях нулевой гипотезы) количество объектов в клетке таблицы, участвующее в построение статистики. Меры связи для номинальных (ранговых) признаков приведены в табл. 3 и табл. 4.

Таблица 1. Оценка современной ситуации в городе

( % от числа ответивших в каждой возрастной группе)