Теория автоматического управления как математическая теория информационных процессов передачи и преобразования сигналов, страница 9

1.  Для системы первого порядка, характеристическое уравнение которой имеет вид

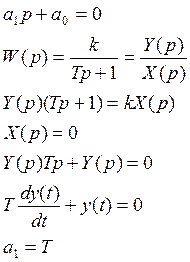
Проверим условие устойчивости Гурвица.

a₁>0, т.к. Т<0 быть не может.

a₀=1, a₀>0, т.е. при любых реальных коэффициентах критерий Гурвица выполняется.

2.  Для системы второго порядка характеристическое уравнение имеет вид

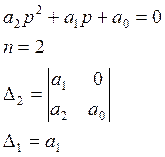
Такая система устойчива только, если Δ₁>0 и Δ₂>0.

Δ₁>0 удовлетворяется, т.к. a₁=2γT, γ>0

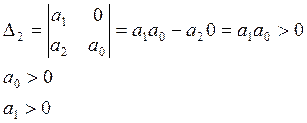
4.4.2 Частотный критерий устойчивости Найквиста

Частотный критерий Найквиста сформулирован в 1936 году, но был засекречен.

Критерий определяет устойчивость замкнутой системы по частотным характеристикам разомкнутой системы.

Существует две альтернативы формулировки этого критерия.

Имеется система

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                          

K(ω) – АЧХ, показывает отношение амплитуды входного сигнала и выходного сигнала, если они синусоидальные.

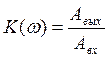
Φ(ω) – ФЧХ, т.е. изменение фазы сигнала при прохождении через систему.

Φ(ω)=φ(ω)

АФХ

 

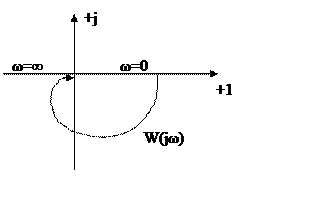1. Замкнутая система устойчива, если  годограф АФХ разомкнутой системы  при изменении частоты от 0 до ∞ не охватывает точку комплексной плоскости Н(-1;j0).                                                                                                                                                                                                                                                                                                                                                                                                                        Эта система является устойчивой.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                              

                                                                                                                                                                                                                                                                                                                                                                                                                                                           Эта система является неустойчивой.

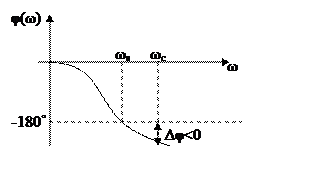
2. Замкнутая система устойчива, если ЛФЧХ разомкнутой системы на частоте среза ω_с имеет положительный запас по фазе Δφ=φ(ω_с)+180^◦, либо ЛАЧХ на частоте ω_s, где φ(ω_s)=-180^◦ имеет положительный запас по амплитуде L(ω_s)<0.

Случай устойчивой системы.

                                                                         ω_c - частота среза

ω_s – частота, на которой фазовый сдвиг разомкнутой системы равен -180^◦

 

В случае неустойчивой системы расположение ЛФЧХ и ЛАЧХ будет следующим

 

Приступим к объяснению данного критерия.

В режиме автоколебаний сигнал ошибки ε(t) можно считать синусоидальным.

Предположим, что система находится на грани устойчивости.

Пусть разомкнутая система вносит фазовый сдвиг

Коэффициент передачи

При этом

 

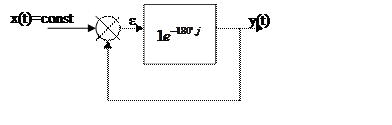Инвертирующий синусоидальный сигнал y(t) совпадает со сдвинутым на 180 градусов сигналом.

 

В условиях положительной обратной связи устойчивость решает коэффициент k.

, то колебания расходящиеся.

, то колебания затухающие.

Проследим выполнение критерия Найквиста на графике ЛФЧХ и ЛАЧХ устойчивой системы.

На частоте возможных автоколебаний ω_s, там, где выполняются фазовые условия самовозбуждения Δφ=0, L(ω_s)< 0-ЛАЧХ разомкнутой системы, поэтому колебания будут затухающими.

На уровне АФХ пограничные условия возбуждения автоколебаний соответствует следующему положению годографа на частоте ω_s

 

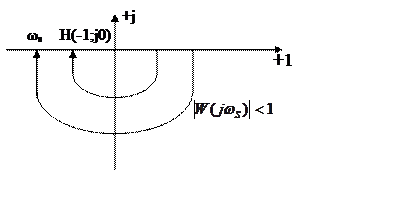Если , то система неустойчива.

Если , то система устойчива.

Преимущество критерия Найквиста по отношению к другим критериям

1.  Можно использовать экспериментально снятые частотные характеристики

2.  Возможность оценки устойчивости для систем, содержащих трансцендентные, иррациональные звенья.

             

 

Если точка Н внутри спирали,

то система неустойчива.

4.5 Построение ЛАЧХ разомкнутой системы

Пусть система имеет следующую структуру

 

Нужно построить ЛАЧХ для разомкнутой системы (системы с разомкнутой обратной связью)

Тогда ЛАЧХ будет иметь следующий вид

, где - АЧХ

Используем свойство логарифмов, тогда получим

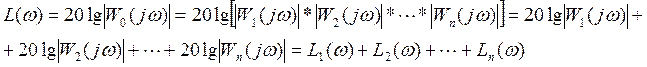
Для нахождения ЛАЧХ разомкнутой системы нужно сложить ЛАЧХ всех звеньев, входящих в прямой канал.