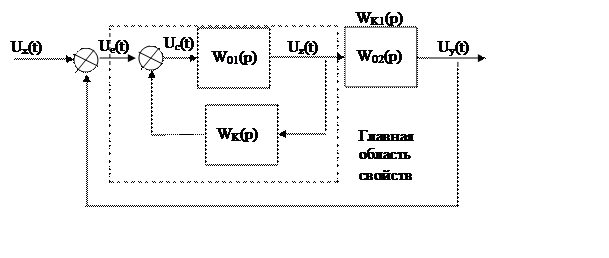
Другие предметы \ Теория автоматического управления

Теория автоматического управления как математическая теория информационных процессов передачи и преобразования сигналов, страница 13

Встречно-параллельное корректирующее устройство

Позволяет использовать один усилительный элемент (как правило усилитель мощности, а свойства системы формируются внешними обратными связями)

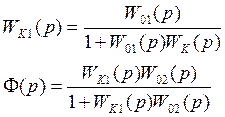
Прямое использование для синтеза неудобно, поэтому их сводят к последовательной коррекции.

Сведение параллельной коррекции к последовательной

Проанализируем WK1

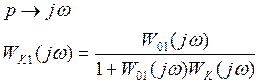
Частоты от 0 до ωС влияют на работу САУ

  (1)

Если ω>ωС, то условие (1) не выполняется, поэтому в существенном диапазоне частот можно пренебречь единицей.

 

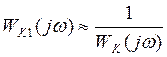
Свойства локальной подсистемы определяются за счет свойств регулятора. Это позволяет прийти к той же структуре, что и при последовательном соединении.

 

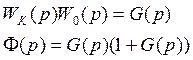
Обычно задаются следующие параметры: W0(p) – объект управления, q – порядок астатизма, KC, KV, KA – добротности, .

Требуется найти WK(p)

Наиболее отработанным методом найдем WK(p)

7.2.1 Синтез корректирующих устройств по методу ЛАЧХ

Требования к объекту:

1.  ЛАЧХ не должна иметь резонансных пиков, это позволяет использовать асимптотическую ЛАЧХ.

 


2.Объект не должен иметь трансцендентного звена запаздывания

Этапы синтеза:

1.  Построение желаемой ЛАЧХ разомкнутой системы Lжел(ω)

2.  Построение в этих же осях ЛАЧХ объекта L0(ω)

3.  определяется корректирующее устройство в виде ЛАЧХ из условия

   

Это условие появилось, потому что Lжел должна получиться последовательным соединением корректирующего устройства и объекта управления. Отсюда  

Как правило, вычислений не требуется, так как по ЛАЧХ можно графически найти необходимые величины.

4.  Переход от ЛАЧХ корректирующего устройства к WK(p).

WK(p) может быть физически нереализуемой величиной. Признаком этого является m>n (порядок полинома числителя n меньше порядка знаменателя m)

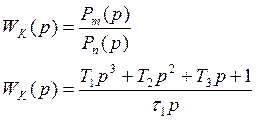
Если n>m, то это реализуемо

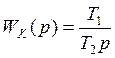
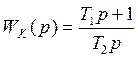 - регулятор ПИ-типа, в нем m=n, что тоже является реализуемым.

Если мы получили нереализуемое устройство, то нужно скорректировать Lжел(ω)

5.  Моделирование системы

Если после моделирования получается иное, чем хочется, то нужно корректировать Lжел.

Правила построения Lжел

Типовой вид Lжел(ω) следующий

 


1. Наклон низкочастотной  (нч) части ЛАЧХ определяет порядок астатизма.

q=0,1,2

q=0          наклон 0 дБ/дек

q=1          наклон -20 дБ/дек

q=2          наклон -40 дБ/дек

2.  Высота низкочастотной асимптоты Lнч определяет добротность системы.

Определять добротность будем на частоте ω=1 рад/с.

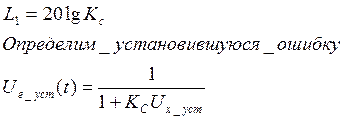
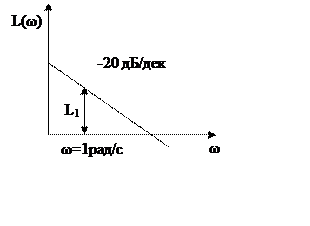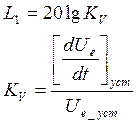
I.                                                           

II.                                                            

III.                                                                     

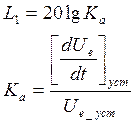
3.  Наклон среднечастотной асимптоты принимается за -20 дБ/дек (ωа-ωв)

Существует теорема о связи ЛАЧХ и ФЧХ:

Если наклон ЛАЧХ на достаточно большом участке частот равен n*(-20) дБ/дек, то ФЧХ на этом же участке частот стремиться к 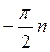 рад.

Примеры:

Ф(р)=k

 


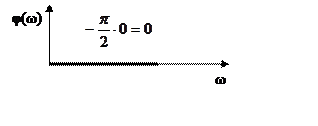                                          n=0, тогда ФЧХ будет иметь вид

        

 


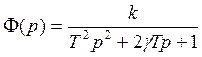
Вернемся к утверждению о использовании -20 дБ/дек

Наклон Lжел=-40 дБ/дек

n=2

Но по критерию устойчивости Найквиста обнаруживаем, что система находится на грани устойчивости, т.к.

Для обеспечения максимально возможного запаса по фазе Δφ наклон желаемой ЛАЧХ в районе частоты среза ωС выбирают равной -20 дБ/дек.

Это не удается сделать из-за наличия хотя бы одного интегратора в системе.

 выбирается достаточно большим (± октава)

Октава – двукратное изменение частоты

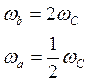
4.  Выбор частоты среза (ЧС)

ЧС определяет быстродействие системы

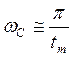
5.  Высокочастотная часть (ВЧ) не оказывает существенного влияния на показания качества.

Это дает нам существенный произвол в выборе ЛАЧХ.

Lжел нужно выбирать таким же как у объекта, с тем чтобы ЛАЧХ корректирующего устройства была по возможности наиболее простой.

7.2.2 Аналитический синтез корректирующих устройств.

Синтез по форме.

1.  задаться желаемой передаточной функцией Фжел(р) системы в соответствии с требуемыми показателями качества. Для этого используются корневые методы. Сущность в том, что корни характеристического уравнения помещаются в требуемое положение на комплексной плоскости, что и обеспечивает желаемое быстродействие и характер переходных процессов.

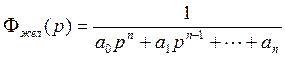
2.  Определить желаемую передаточную функцию разомкнутой системы

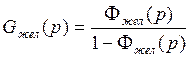
3.  Найти передаточную функцию корректирующего устройства

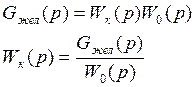
4.  Моделирование системы

Если показатели качества не обеспечиваются, то перейти к пункту 1.

Выбор желаемой передаточной функции замкнутой системы.

Фжел(р)=?

n – порядок системы

Ограничим порядком астатизма q=1

В общем случае знаменатель имеет вид

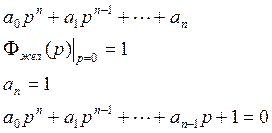
Обозначим корни характеристического уравнения р1…рn

Для удобства задания быстродействия введем понятие среднегеометрического корня (СГК)

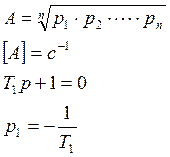
СГК связан с a0 следующим соотношением

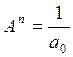 по теореме Виета

Разделим Фжел(р) на а0, тогда получим

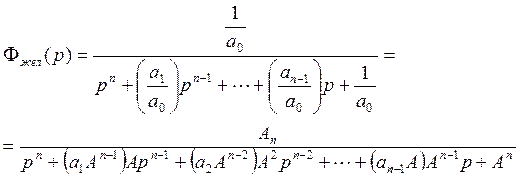
В итоге получим

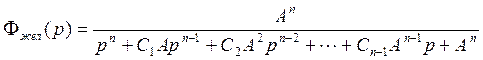
В этом выражении коэффициент , где k=1,2,…n-1.

Коэффициент Сk безразмерный.

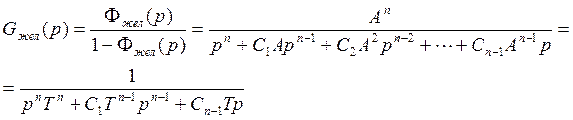
Где Т – базовая постоянная времени

Порядок выбора желаемой передаточной функции

1.  Определить порядок n желаемой передаточной функции

, где n0 порядок объекта.

2.  выбрать определенный способ распределения корней на комплексной плоскости.

 


3.  Определить коэффициент Сk в характеристическом уравнении.

4.  Определить величину среднегеометрического корня или базовую постоянную времени Т, исходя из требуемого быстродействия системы (обычно оно задано по времени переходного процесса)

 

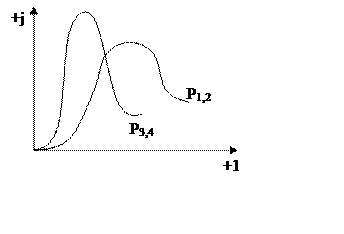
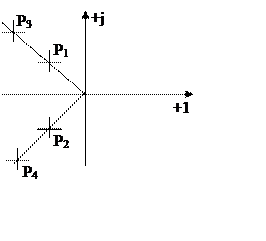
7.2.3 Аналитический синтез при биномиальном распределении корней

 

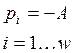
Такая настройка характеризуется гарантированным отсутствием перерегулирования.

                                                        

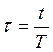
  T выбирается на заключительном этапе проектирования, исходя из заданного времени процесса.

Скачать файл