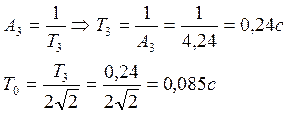
Т0 задает масштаб по времени в процессе, зафиксированном в универсальной кривой h4.
Форма кривой не изменится при любом значении Т0.
Итог синтеза
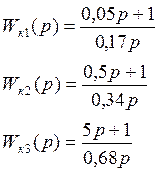
Мы получили три простых однотипных регулятора, вместо одного сложного.
8.Цифровые автоматические системы
Структура аналогового управляющего устройства

Вычислительное устройство осуществляет преобразование информации на уровне формализованной оценки сигналов, т.е. кодов.
![]()
Все остальные операции преобразования информации легко сводятся к арифметическим действиям над кодовыми сигналами.
Структура вычислительно-управляющего устройства будет подобна структуре аналогового устройства с дополнениями
 |
Микро-ЭВМ работает по программе, реализуя многие функции, которых не было в аналоговом регуляторе.
Функции:
1. Обслуживание датчиков
2. Обслуживание ЦАП (цифро-аналогового преобразователя)
3. Обслуживание устройств индикации и управления
8.1 Алгоритмы цифрового управления
Устройство распадается на:
А) Собственно алгоритмы управления, которые необходимо выполнять с жестко фиксированной периодичностью (периодом квантования), в остальном математическое описание полностью повторяет аналоговые алгоритмы (обслуживание датчиков)
Б) Фоновые алгоритмы – обслуживание клавиатуры и индикации, самодиагностика и т.д., допустимо прерывание
Т.о. диаграмма загрузки процессора будет иметь вид
 |
Недостаток:
1. Квантование по уровню
2. Дискретный характер сигналов
 |
|||
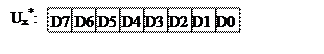 |
|||
![]() - разрешающая способность ЦАП
- разрешающая способность ЦАП
8.2 Квантование по уровню и времени
8.3 Математическое описание цифровых элементов систем управления
Дискретное преобразование Лапласа (z- преобразование)
Дискретным преобразованием Лапласа мы будем называть величину
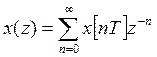 , где x[nT] –
решетчатая функция, получаемая путем выделения ее значений в дискретные моменты
времени
, где x[nT] –
решетчатая функция, получаемая путем выделения ее значений в дискретные моменты
времени
Т – период квантования

z – оператор дискретного преобразования Лапласа
![]()
Т – период квантования по времени
р – параметр преобразования Лапласа
Связь дискретного преобразования Лапласа и обычного преобразования Лапласа
Представим себе последовательность δ – импульсов, площадь которых пропорциональна значениям решетчатой функции

![]()
nT – смещение
Каждая функция ![]() при
изменении времени t от 0 до ∞ вносит в эту сумму свой вклад только один
раз, когда время равно смещению.
при
изменении времени t от 0 до ∞ вносит в эту сумму свой вклад только один
раз, когда время равно смещению.

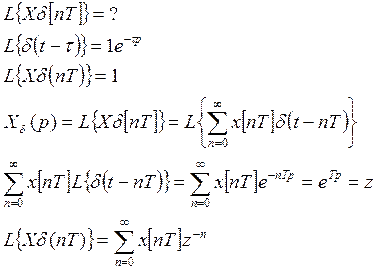
Обычное преобразование Лапласа от последовательности импульсов
![]() промодулировано значениями
решетчатой функции и является дискретным преобразованием Лапласа.
промодулировано значениями
решетчатой функции и является дискретным преобразованием Лапласа.
Это необходимо для того, чтобы математическое описание цифровых систем выполнялось теми же средствами, что и для аналоговых систем.
При этом сигналы в цифровых системах (коды) нужно представлять себе как последовательности δ-импульсов.
Таблица соответствия непрерывной функции обычного преобразования Лапласа и z-преобразования Лапласа
|
x(t) |
X(p) |
x[nT] |
X(z) |
|
δ(t) |
1 |
δ[nT] |
1 |
|
δ(t-τ) |
|
|
|
|
1(t) |
|
1[nT] |
|
|
t |
|
nT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основные свойства дискретного преобразования Лапласа:
1. Свойство линейности
![]()
2. Сдвиг оригинала во времени.
Изображается умножением z-преобразования на множитель z-k, где k – число тактов сдвига.
![]()
Существуют теоремы о начальном и конечном значении оригинала, которые нам не понадобятся.
8.4 Разностные уравнения
Представим себе цифровую систему управления, на входе которой действует x[nT].
 |
Для линейных алгоритмов цифрового управления выходная последовательность кодов связана с входной разностным уравнением
![]() В этом
уравнении r, l, m, n – целые числа.
В этом
уравнении r, l, m, n – целые числа.
L=r-m – показывает на последний сформированный регулятором отчет.
 |
Все линейные алгоритмы могут быть описаны таким разностным уравнением, поэтому оно имеет общий характер, справедливый для любых алгоритмов.
8.5 Дискретная передаточная функция
Возьмем z-преобразование от левой и правой части разностного уравнения, записанного в предыдущем параграфе. Будет использоваться свойство линейности и теорема о сдвиге оригинала, поэтому каждое слагаемое будет иметь множитель, отображающий сдвиг этого слагаемого.
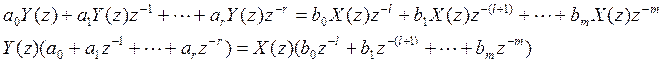
Дискретная передаточная функция будет иметь вид
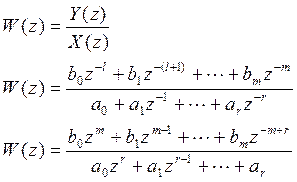
Понятие дискретной передаточной функции введено только для нулевых значений начальных условий.
![]()
8.6 Переход от дискретной передаточной функции к разностному уравнению
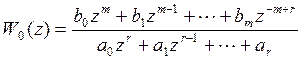
 |
1. Преобразуем дискретную передаточную функцию к следующему виду
![]()
2. 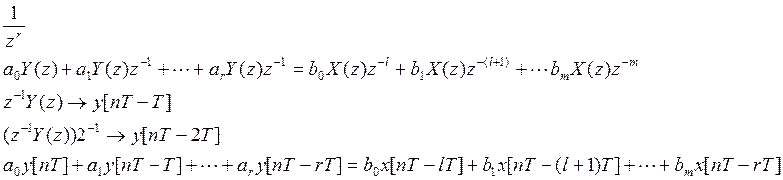 Уединим в левой
части выходной сигнал на текущий момент времени.
Уединим в левой
части выходной сигнал на текущий момент времени.
Y[nT] – выходной сигнал на текущий момент времени
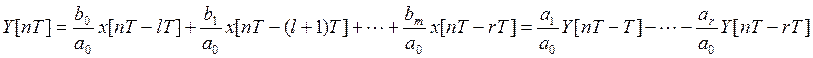 Алгоритм работы
цифрового регулятора:
Алгоритм работы
цифрового регулятора:
1. Выставляет входной сигнал на l ходов вперед, приформировывает еще на 1 шаг раньше сигнал вплоть до r шага.
2. Компонента
Регулятор –рекуррентное возвратное уравнение
8.7 Условия физической реализуемости цифрового регулятора
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.