Теория автоматического управления как математическая теория информационных процессов передачи и преобразования сигналов, страница 14

Теорема Безу

                                                                                        бином Ньютона

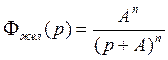
n	Фжел(р)
1
2
3
4

                    1

n=1           1    1

n=2         1   2   1

n=3       1   3   3   1

n=4     1   4   6   4   1

n=5   1  5  10  10  5   1

7.2.4 Аналитический синтез при распределении корней по Баттерворду (Настройка системы на модульный оптимум)

При этом модуль частотной характеристики в окрестности частоты среза будет минимальным. Модули всех корней одинаковы и равны А. Сами корни располагаются на окружности радиуса А в левой полуплоскости.

Если n – четное, то все корни комплексные (n/2 симметрично расположенных корней)

Если n – нечетное, то один действительный корень, остальные комплексно сопряженные.

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                 

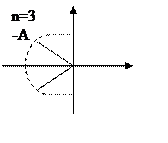
n	Фжел(р)	Pi корень характеристического уравнения
1
2
3
4

                      Подобранные Баттервордом значения

Универсальные переходные функции системы

n	1	2	3	4
	-	4,44	5	6,36
	3	3	6	7,2
	-	4,3	8	6,2

 

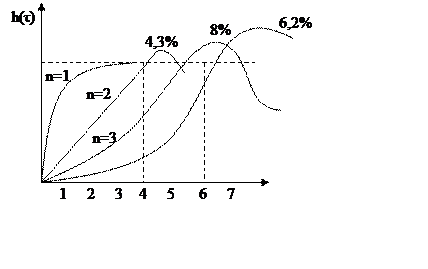
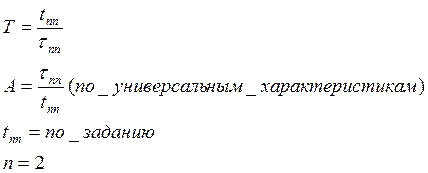
7.2.5 Пример синтеза регулятора аналитическим методом

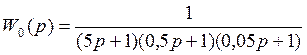- объект

Выполним синтез регулятора, при этом обеспечиваем настройку на модульный оптимум, причем время достижения максимума t_max=1,5 с.

1.  n=3

h(τ)              τ_max=5

2.

     

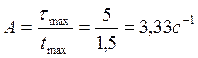
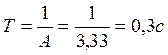
3. Желаемая передаточная функция замкнутой системы

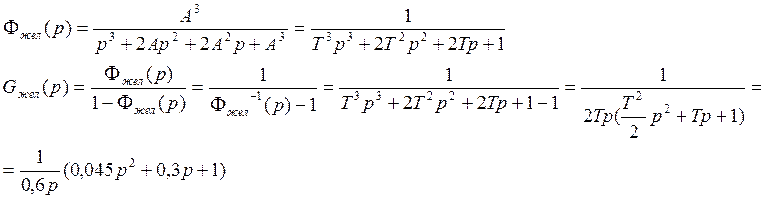4. Синтез регулятора (корректирующее устройство)

G_жел(р):

 

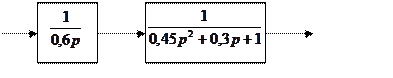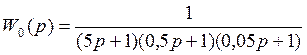
Основное уравнение синтеза

 

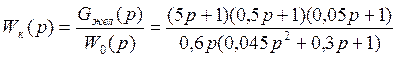
7.2.6. Пример аналитического синтеза многоконтурной системы

Поскольку точность регулятора обусловлена сложностью объекта (знаменатель объекта попадает в числитель регулятора), то нужно разбить синтез на несколько этапов, причем на каждом этапе включают только простой подобъект. Это можно сделать, если система будет многоконтурной.

 

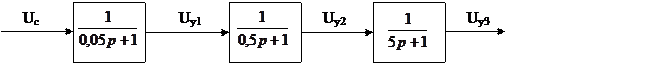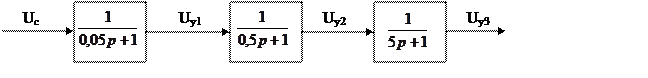U_y1 и U_y2 – сигналы датчиков промежуточных регулируемых величин.

По каждой регулируемой величине введем свое регулирующее устройство и свою обратную связь.

 

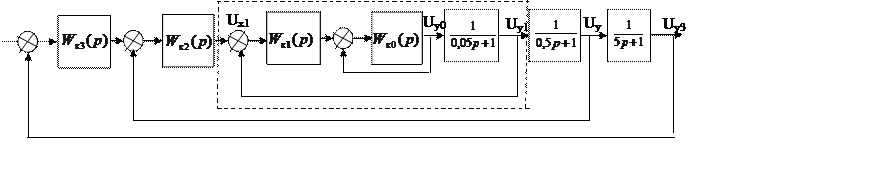
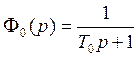 - назначение задать T₀ (базовую постоянную времени). Если его не вводить, оно все равно появится в регуляторе, но в технике регулирования вводят его в явном виде для ограничения полосы пропускания.

Такие структуры называются системами подчиненного регулирования.

Далее поконтурно синтезируем корректирующее устройство.

Порядок первого контура (выделенного на рисунке пунктиром) n=2.

Желаемая передаточная функция при распределении корней по Баттерворду

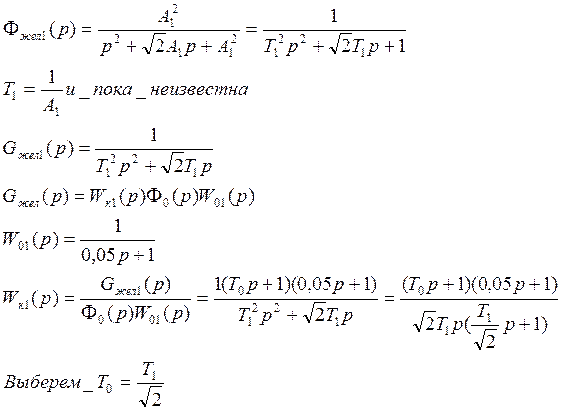
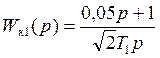
Выразим Т₁ через Т₀

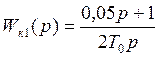    - пропорционально-интегральный регулятор (ПИ-                регулятор)

 

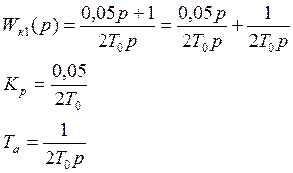
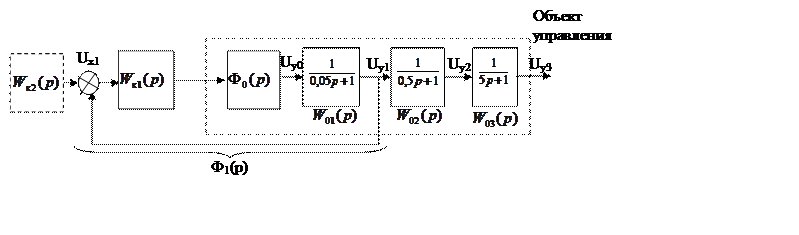
Изобразим структурную схему первого контура

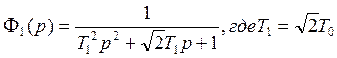
Займемся синтезом регулятора второго контура. Будем полагать, что замкнутый контур Ф₁(р) является частью объекта, т.е. его синтезировать не будем.

                                                                                                                                                                                                                                                                                                                                                                                                                                                                         

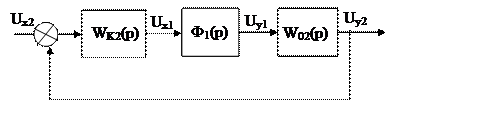
Выбираем желаемую передаточную функцию второго контура исходя из распределения корней по Баттерворду.

Передаточная функция получается не менее третьего порядка.

Выберем желаемую передаточную функцию для n₂=3

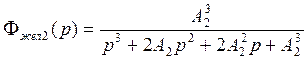
Введем обозначение базовой постоянной второго контура

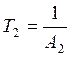
Тогда Ф_жел2(р) будет иметь вид

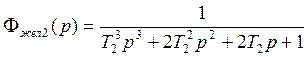
Тогда желаемая передаточная функция разомкнутого контура находится как

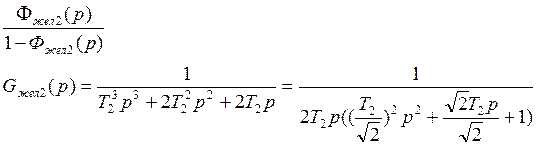
Потребуем:

1.  G₂(p)=G_жел2(p)

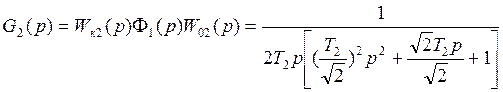
2.

3.

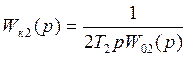
Корректирующее устройство второго контура должно компенсировать инерционность второго подобъекта.

Регулятор W_к2 вносит интегратор во второй контур с постоянной Т₂.

Интегратор обеспечивает заданный порядок астатизма q=1, а постоянная Т₂  связанная с Т₁ обеспечивает настройку на модульный оптимум.

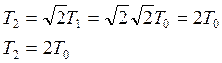
Получим передаточную функцию регулятора второго контура в явном виде

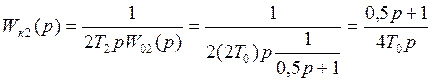 - пропорционально-интегральный регулятор будет компенсировать подобъект второго контура.

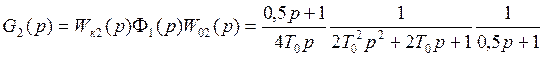
В передаточной функции разомкнутого контура регулятор компенсирует («уничтожает») объект.

Синтез регулятора третьего контура

Структурная схема

 

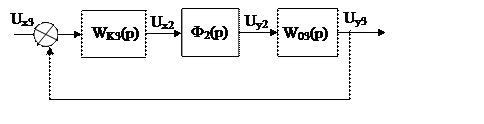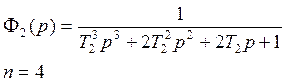
Ф_жел3(р) должна быть четвертого порядка

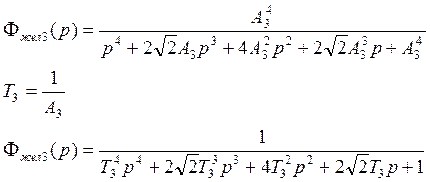
Синтез регулятора

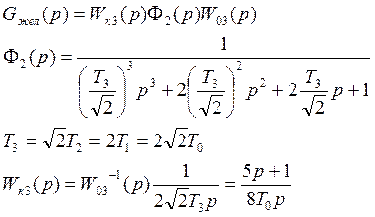
Расчет регулятора

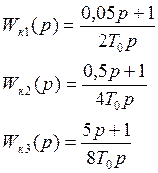
Определим Т₀ исходя из требуемого быстродействия системы.

 

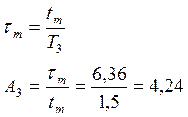
Средний геометрический корень А₃ выявлен для обеспечения t_m=1,5 с.