Теория автоматического управления как математическая теория информационных процессов передачи и преобразования сигналов, страница 7

                                                где Т – постоянная времени интегрирования

4.Весовая функция

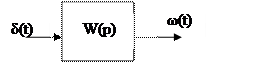
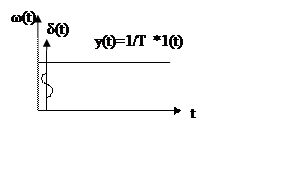
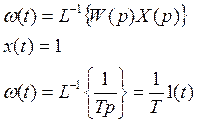
5. Частотная характеристика

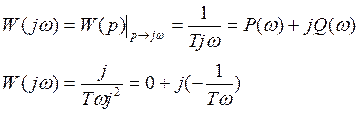
P(ω)=0

Q(ω)=-1/Tω

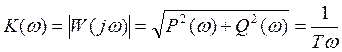
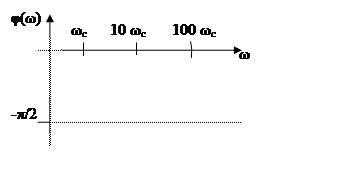
7.ФЧХ

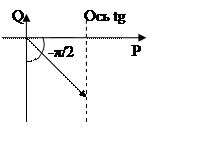
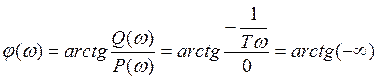
Синусоидальный сигнал любой частоты интегратор сдвигает на –π/2

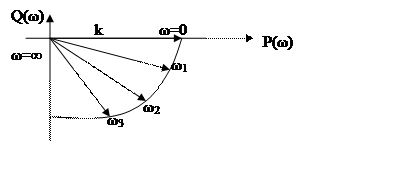
Годограф частотной характеристики.

 

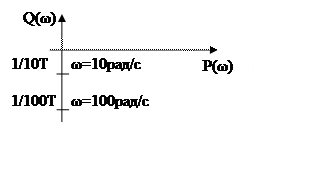
8.ЛАЧХ

k=1

ω_с-частота среза, т.е. звено перестает усиливать входящий синусоидальный сигнал

 

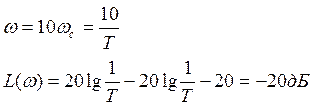
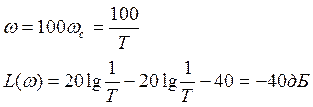
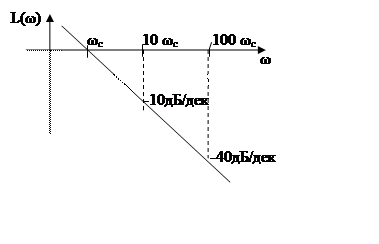
9.ЛФЧХ

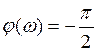
3.7  Апериодическое звено (инерциальное звено первого порядка)

1.Передаточная функция

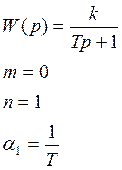
2.Дифференциальное уравнение

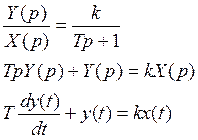
Пример:

Рассмотрим RC-цепь

Uвх

Uвых(t)

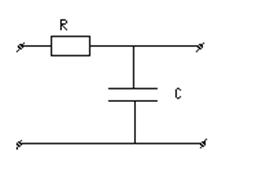
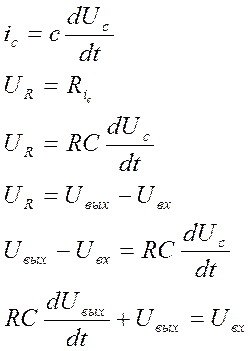
3.Переходная функция

x(t)=1(t)

	x(t)

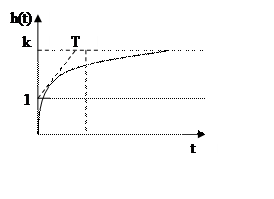
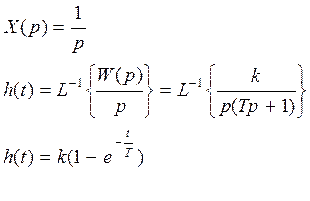
Т-характеристика инерционности

Т - постоянная времени апериодического звена

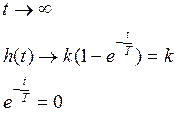
k-коэффициент передачи установившегося значения по амплитуде

Yуст=kХуст

4.Весовая функция

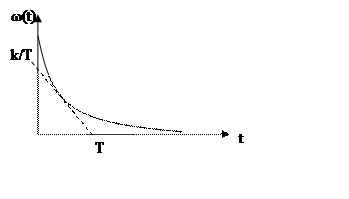
5.Частотная характеристика

Для получения комплекснозначной частотной характеристики используем передаточную функцию.

 

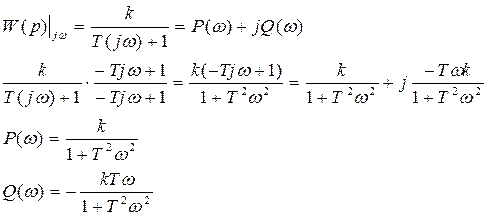
6.АЧХ

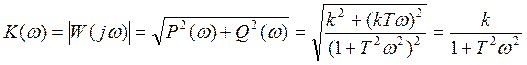
7.ФЧХ

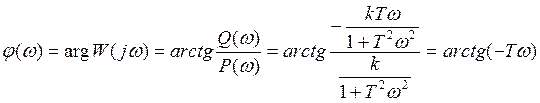
8.ЛАЧХ

Асимптотические (предельные) характеристики

                                                 y=1/x

8.1Рассмотрим низкочастотные характеристики ЛАЧХ

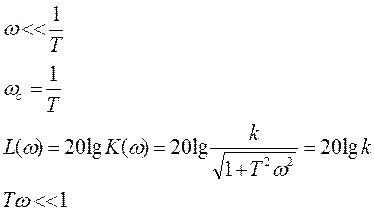
8.2 Рассмотрим высокочастотные характеристики ЛАЧХ

 

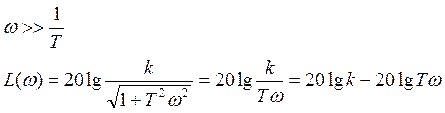
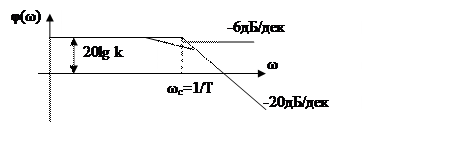
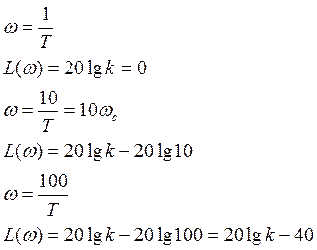
В инженерной практике пользуются исключительно асимптотическими характеристиками.

9.ЛФЧХ

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   

 

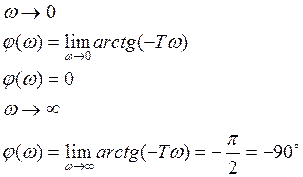
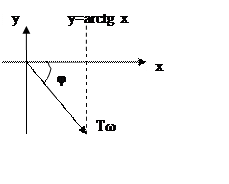
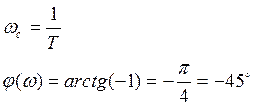
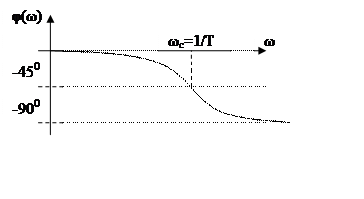
10.Годограф

                                  

3.8  Дифференцирующее звено

1.Передаточная функция

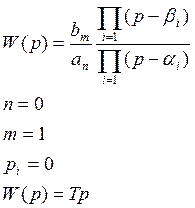
2.Дифференциальное уравнение

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                

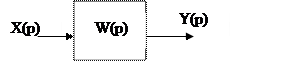
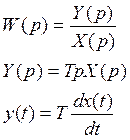
Чисто дифференциальных звеньев в природе не существует, есть звенья, которые являются частично дифференцирующими.

Пример:

Пусть используется датчик скорости – тахогенератор

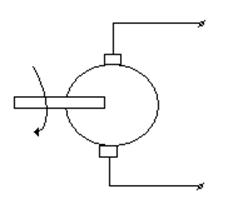
Y(t)=U(t)

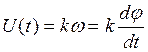
3.Переходная функция

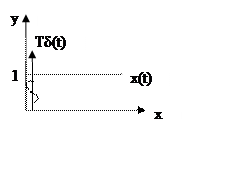
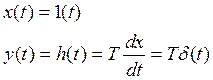
4.Весовая функция

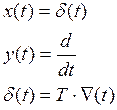
Ñ(t) является набла функцией.

5.Частотная характеристика

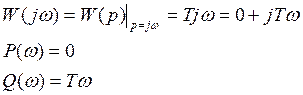
6.АЧХ

7.ФЧХ

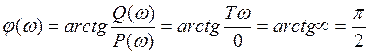
8.ЛАЧХ

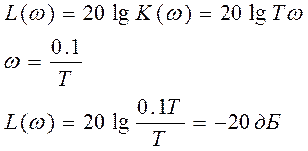
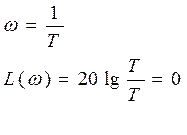
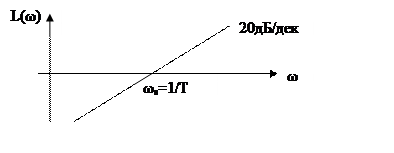
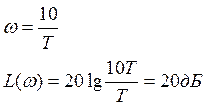
ω_S – частота среза

k=1

L(ω_S)=0

Реальный сигнал содержит помехи. Спектр помехи всегда существенно шире, но амплитуда меньше, чем у полезного сигнала.

Дифференциальное звено усиливает помехи тем сильнее, чем выше их частота, в результате соотношение сигнал-шум ухудшается.

9.ЛФЧХ

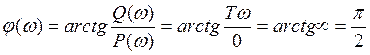
10.Гадограф

3.9  Форсирующее звено

1.Передаточная функция

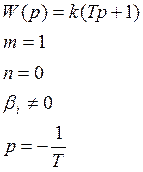
2.Дифференциальное уравнение

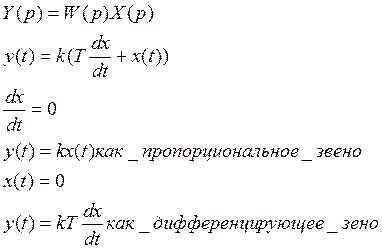
k – коэффициент усиления

Т – постоянная времени дифференцирования

3.Переходная функция

h(t)=h_диф(t)+h_проп(t)=kTδ(t)+k1(t)

4.Весовая функция

ω(t)= ω_диф(t)+ ω_проп(t)=TÑ(t)+kδ(t)

5.Частотная характеристика

P(ω)=k

Q(ω)=Tkω

6.АЧХ

7.ФЧХ

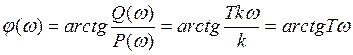
8.ЛАЧХ

8.1 Низкочастотные характеристики

ω<<1/T

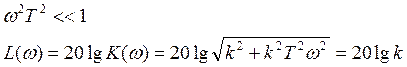
8.2 Высокочастотные характеристики

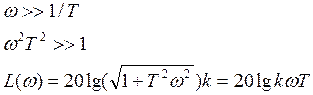
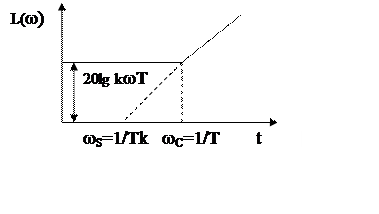ЛАЧХ имеет такой же вид как и у дифференцирующего звена.

9.ЛФЧХ

 

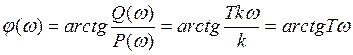
10.Годограф

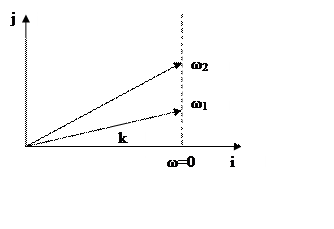                                                                 ω₂ > ω₁ > 0

3.10 Колебательное звено

1.Передаточная функция

T-постоянная времени собственных колебаний

γ-коэффициент демпфирования

k-коэффициент передачи установленного значения

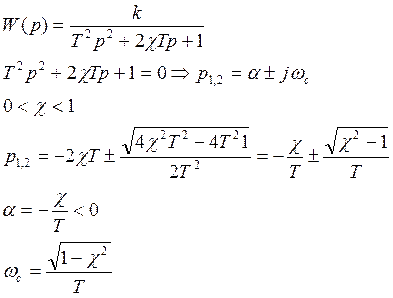
2.Дифференциальное уравнение

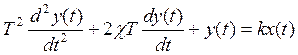
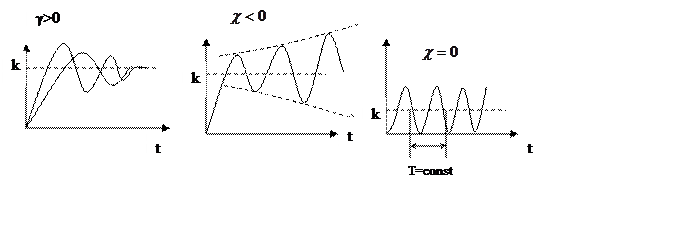
3.Переходная функция

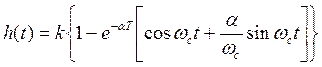
4.Весовая функция

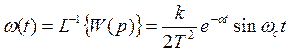
5.Частотная характеристика

 

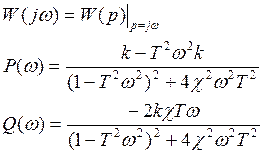
6.АЧХ

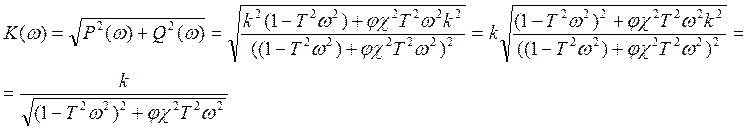
Асимптотические АЧХ

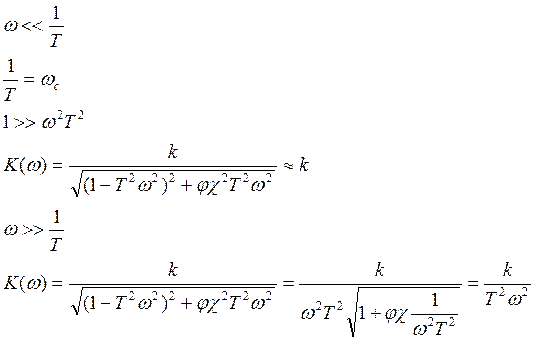
7.ФЧХ

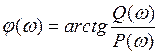
φ(ω) – зависимость изменения фазы синусоидального сигнала, прошедшего через звено.

 

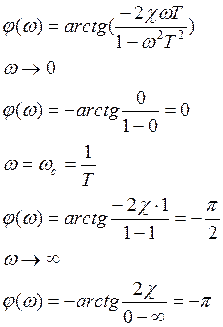
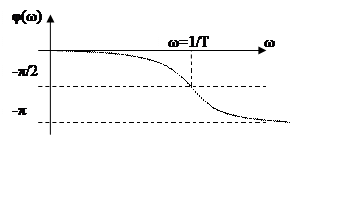8.ЛАЧХ

8.1. Низкочастотные ЛАЧХ

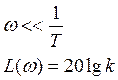
8.2. Высокочастотные ЛАЧХ

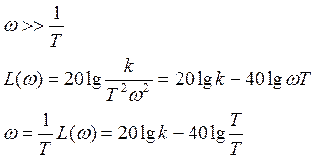
10. Годограф

 

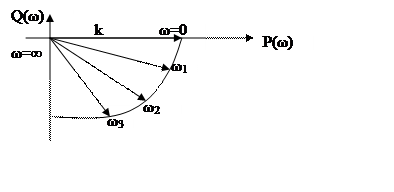3.11.Звено частого запаздывания (транспортного)

Звено частого запаздывания – звено, которое воспроизводит входной сигнал с задержкой τ.

 

Для определения W(p) необходимо уравнение, которое имеет следующий вид:

Задержка τ всегда положительна. Если τ<0, то тогда бы сигнал являлся на выходе раньше, чем на входе. Отсюда вытекает принцип каузальности (причинности), который запрещает τ<0.

1.Передаточная функция

по теореме о смещении изображения получим

Отсюда следует, что

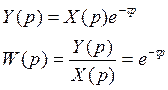
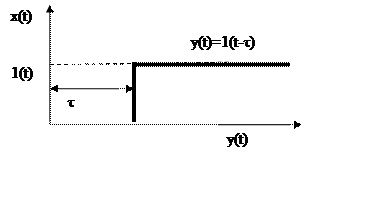
3.Переходная функция

Если x(t)=1(t), то h(t)=1(t-τ)

Графически это имеет следующий вид

                                                                                                                                                   

4.Весовая функция

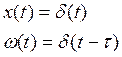
δ-функция – функция, которая выдается в момент t=0.

Для t=τ аргумент δ-функции U=t-τ=0

График функции

 

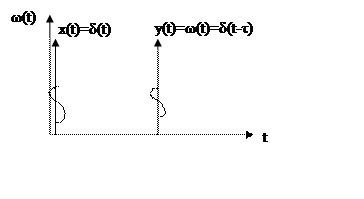
5.Частотная характеристика

Частотная характеристика у этого звена не выразительная.

Из этого следует, что

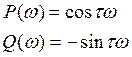
где ω-круговая частота синусоидального входного сигнала.