Теория автоматического управления как математическая теория информационных процессов передачи и преобразования сигналов, страница 3

Построение такой системы требует теоретического обоснования, это обоснование дал Вишнеградский 1795 году.

Он показал, что существует область устойчивости в работе данной машины.

mгрузов

m

Машина

Ркотла

          2 Математическое описание линейных систем

автоматического управления

Далее рассмотрим математическое описание линейных систем автоматического управления – построение математических моделей элементов и звеньев, обладающих свойством линейности

2.1 Линейные звенья автоматических систем

Будем считать, что все звенья описываются дифференциальным уравнением.

Обычно дифференциальные уравнения системы записываются в таком виде, что значения регулируемой величины и ее производных располагаются в левой части уравнения. Значения входных воздействий (управляющих и возмущающих) и их производных располагаются в правой части.

Представим звено следующим образом:

 

Тогда полное дифференциальное уравнение будет иметь следующий вид:                                                                                                                     

        (*)

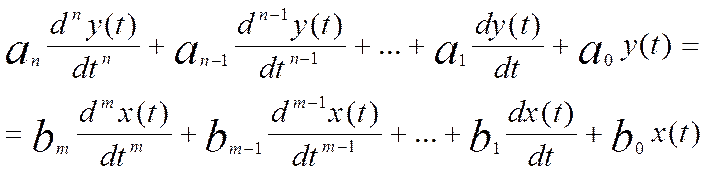Пример

Редуктор – механизм из нескольких зубчатых колес для передачи вращения от одного вала к другому.

Дадим математическое описание редуктора как элемента автоматической системы.                                 

          

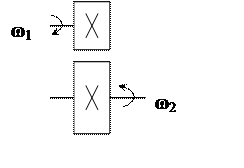
                                                                ω₁(t)    ω₂(t)

                                                                 

                                                                                                                   =>

=>

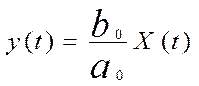
Пример математического описания элемента системы.

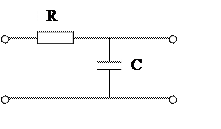
Рассмотрим следующую электрическую цепь

Uвых=Y(t)

Uвх=X(t)

ic

 

                                                                         

                                                                          

     

                                                               

 

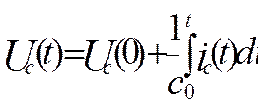
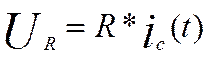
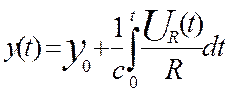
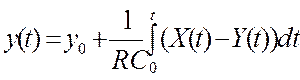
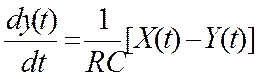
a₁=RС

a₀=1              

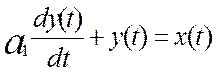
b₀=1         

Это уравнение описывает инерционное звено первого порядка (апериодическое)

x(t)

y(t)

 

Линейными называются звенья, обладающие следующим свойством:

Пусть реакция на сигнал X₁(t) выглядит, как Y₁(t), а сигналу X₂ соответствует

сигнал Y₂

X=X₁(t)       Y=Y₁(t)

X=X₂(t)       Y=Y₂(t)

X=X₁(t)+X₂(t) может быть найдена, как Y=Y₁(t)+Y₂(t)

 

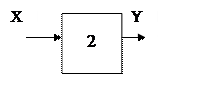
                               Докажем, что звено (редуктор) является линейным:

                                X₁=2                       Y₁=4                       

                                X₂=3                       Y₂=6

                                X₃=X₁+X₂ =5         Y₃=Y₁+Y₂ =10

Можно показать, что звенья, описываемые уравнением (*) обладают свойством линейности, если коэффициенты a₁,…,a_n=const и  b₁,….,b_n =const

2.2 Типовые сигналы систем автоматического направления.

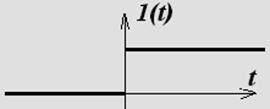
I.  Единичный ступенчатый сигнал                                                                               

      Физически это сигнал замыкающего контакта (релейный сигнал)  

X(t)=1(t)=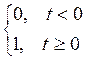

Это функция называется функцией Хевисайда.

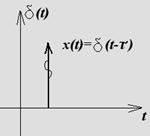
II Импульсная дельта функция (функция Дирака)

Будем называть d-функцией такую функцию, которая обладает следующими свойствами:

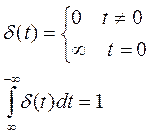
Дадим другое определение d - функции, как пределу последовательности приближений.     

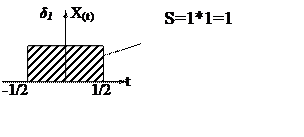Первое приближение.                                

δ ₁=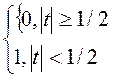

Второе приближение.                                                                

 δ ₂=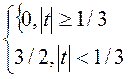                                                                       

Приближение  п - порядка

δ _n=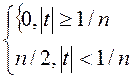

Площадь графиков каждого приближения постоянна и равна 1.

 называется предел последовательности прямоугольных импульсов, которые строятся по следующему правилу:

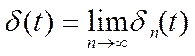
IIIЛинейно изменяющийся сигнал

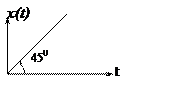X(t=)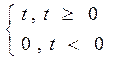   

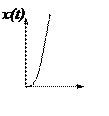IVПараболический сигнал

x(t)=

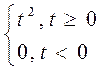
Применяется в задачах исследования точности автоматических систем.

VГармонический(синусоидальный сигнал) сигнал

 

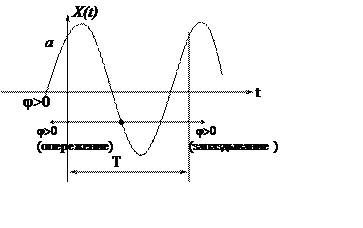Описывает соотношение:

X(t)=asin(wt+j)

          a-амплитуда

          j- начальная фаза

          Т – период.(время, через которое

 значение функции повторяется)

¦=1/T - циклическая частота (число периодов в секунду)

w = 2p*¦  - круговая (угловая) частота. Угловая частота показывает сколько периодов в радианной мере укладывается в единицу измерения.

X(t + T)=x(t)

ƒ=1/T

ω=2πƒ, где ω – угловая частота.

VIОбобщенный гармонический сигнал

Тоже синусоидальный сигнал, представленный в комплексной форме.

k=a+jb – алгебраическая форма записи комплексного числа, где

 а - действительная составляющая

 jb- мнимая составляющая         

k =M(cosφ+jsinφ)-тригонометрическая форма записи комплексного числа

k=M*e^jφ- показательная форма записи комплексного числа

-длина вектора

φ=arctgb/a

 

φ=ωt;      ω=2π/T;  b=M*cosφ=M*cosωt

М – длина вектора

b – действительная часть

X2(t)

а – мнимая часть

Формула Эйлера:

e^jφ= cosφ+jsinφ

X₁(t)-синусоидальный,X₂(t)-синусоидальный, но с другой амплитудой.

X₁=X_1mcosωt

X₂=X_2mcos (ωt+ φ)

Представим входной сигнал в виде суммы двух комплексных чисел.