L(ω)=20 lg k(ω)
ЛАЧХ измеряется в децибелах (дБ)
|
k |
0,001 |
0,01 |
0,1 |
1 |
10 |
100 |
1000 |
|
L, дБ |
-60 |
-40 |
-20 |
0 |
20 |
40 |
60 |
|
Эффект |
ослабление |
равенство |
усиление |
||||
Смотря на ЛАЧХ, говорят, что сигнал изменился на несколько децибел.
k показывает во сколько раз изменился сигнал.
Таким образом, L(ω) является аддитивной оценкой порядка изменения сигнала.
L(ω)=10 lg k2(ω)
L(ω) является энергетической оценкой, так как интенсивность колебаний пропорциональна квадрату.
Изменение амплитуды на один децибел соответствует
изменению сигнала в ![]() раз.
раз.
Ось частот представляется в логарифмическом масштабе, при этом нулевая частота оказывается в -∞
ω=0, L(ω)=lg ω=-∞
За начало отсчета в логарифмическом масштабе нужно
принять произвольную частоту ![]()
Все частоты, отстоящие от ω0 в равное число раз, в логарифмическом масштабе будут изображаться равными интервалами частот. За меру такого отстояния принимается декада (10).
Таким образом, ωх будет находиться на расстоянии х от ω0.
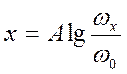 , где ω0-начало
отсчета
, где ω0-начало
отсчета
А-масштаб частоты в логарифмическом измерении, измеряется в мм/дек.
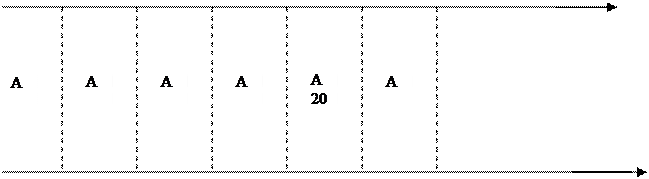
Пример
ω0=1 рад/с А=20 мм/дек
|
 |
|
![]()
![]()
|
Порядок построения логарифмической оси частот:
1. Выбрать начальную частоту ω0
2. Выбрать масштаб по частоте (А) исходя из интервала частот, который хотим представить и размера рисунка.
3. Разграфить ось частот, пользуясь унифицированным соотношением
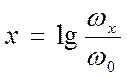
|
ωх/ω0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Lg ωх/ω0 |
0 |
0.3 |
0.48 |
0.6 |
0.7 |
0.78 |
0.85 |
0.9 |
0.95 |
1 |
|
Необходимо помнить, что в логарифмическом масштабе промежутки разные.
Асимптотические ЛАЧХ
Асимптотические ЛАЧХ - это прямые, приближенно заменяющие криволинейные частотные характеристики L(ω), φ(ω) в логарифмическом масштабе.
В данном случае L(ω) и φ(ω) будут называться диаграммами Боде.
3.Характеристики типовых линейных звеньев.
3.1 Типы соединения линейных звеньев.
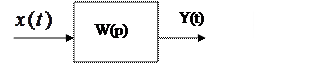 |
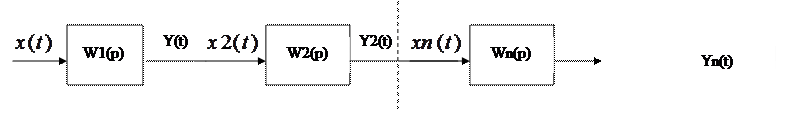 |

W(p)=W1(p)*W2(p)*…*W3(p) (**)
W(p)=Y(p)/X(p)
W1(p)=Y1(p)/X1(p)
W2(p)=Y2(p)/X2(p)
…
Wn(p)=Yn(p)/Xn(p)
W1(p)*W2(p)*…*Wn(p)=Y1(p)/X1(p) * Y2(p)/X2(p) * … * Yn(p)/Xn(p)
По свойству пропорции получаем
Y1(p)=X2(p), Y3(p)=X3(p)

W(p)=Yn(p)/X1(p) (**)
Пример
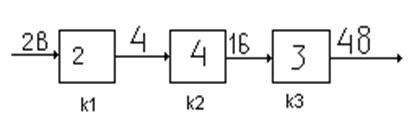
k0=k1*k2*k3=2*4*3=24
Uвкл=k0Yвх=483
3.2Параллельное соединение линейных звеньев
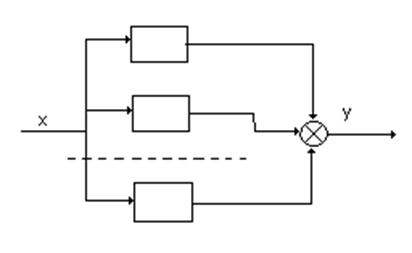
W(p)=Y(p)/X(p)
W(p)=W1(p)+W2(p)+…+Wn(p)= [Y1(p)+Y2(p)+…+Yn(p)]/X(p)= 1/X(p)*( Y1(p)+Y2(p)+…+Yn(p))=Y0(p)/X(p)=W(p)
![]()
W(p)=Y0(p)/X(p)
3.3 Антипараллельное соединение линейных звеньев
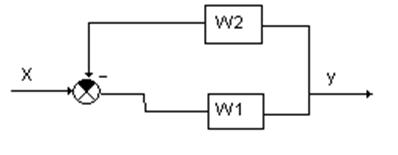
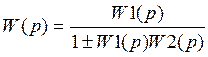
Обозначим выходной сигнал суммирующего элемента как ε
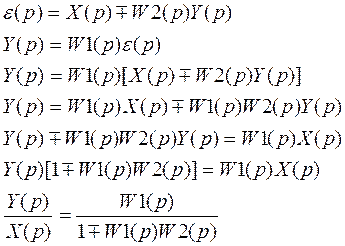

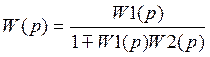 (***) Формула замыкания системы
(***) Формула замыкания системы
Знак + в формуле (***) соответствует отрицательной обратной связи, а знак – соответствует положительной обратной связи.
3.4 Общий порядок анализа элементарных звеньев
Звеном называют математическую модель элемента, соединения элементов или любой части системы. Звенья, как и системы, могут описываться дифференциальными уравнениями довольно высокого порядка, и в общем случае их передаточные функции могут быть записаны в виде
W(p)=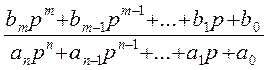
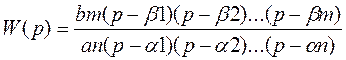
n – порядок системы или звена.
 Общий порядок анализа
элементарных звеньев
Общий порядок анализа
элементарных звеньев
1. Находим передаточную функцию
2. Составляем дифференциальное уравнение
3. Находим переходную функцию
4. Находим весовую функцию
5. Частотная характеристика
6. АЧХ
7. ФЧХ
8. ЛАЧХ
9.ЛФЧХ
3.5 Звено пропорционального усиления (безинерциональное)
Пропорциональным называют звено, которое описывается уравнением y(t)=ku(t), или, что то же, передаточной функцией W(p)=k.
1.Передаточная функция:
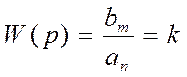 , где ai=0 i=1..n
, где ai=0 i=1..n
bj=0 j=1..m
2.Дифференциальное уравнение:
y(t)=kx(t)
 k
k
3.Переходная функция:
x(t)=1(t)
y(t)=h(t)=k*1(t)
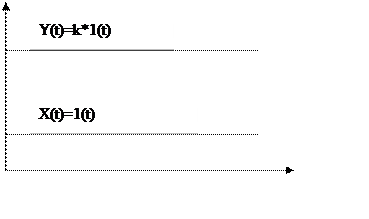
|
4.Весовая функция:
x(t)=δ(t)
y(t)=kx(t)=kδ(t)
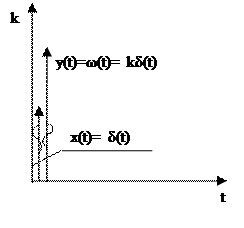 |
5.Частотная характеристика
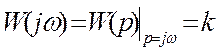
k=P(ω)+jQ(ω)
P(ω)=k
Q(ω)=0
6.АЧХ
![]()
7,ФЧХ
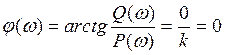
Фазовый сдвиг равен нулю.
|
|
|
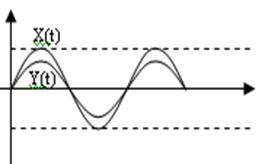
8.ЛАЧХ
L(ω)=20lg k
k=const
|
 |
|
|
|
9.ЛФЧХ
|
 |
|
Пример:
Электрический делитель (потенциометр)
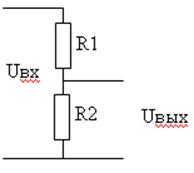
![]()
Uвых=R2*Uвх/(R2+R1)=k*Uвх
k<1
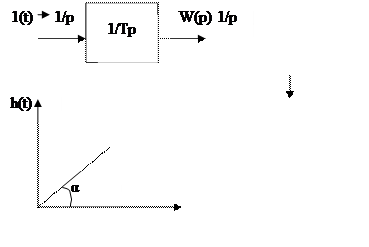
3.6 Интегрирующее звено
1. Передаточная функция
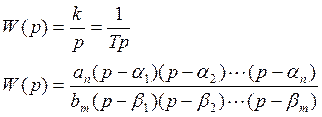
T - постоянная интегрирования
Если αi=0, n=0, βi=0, n=1
2.Дифференциальное уравнение
 |

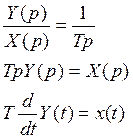
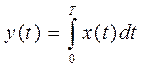
3,Переходная функция
x(t)=1(t)
h(t)=y(t)
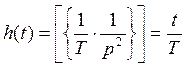
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.