Теория автоматического управления как математическая теория информационных процессов передачи и преобразования сигналов, страница 4

 

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                            

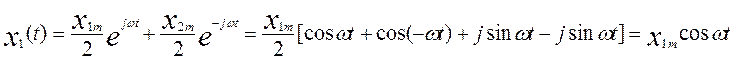
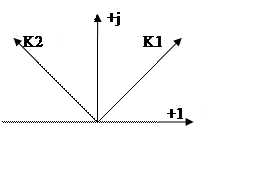
Представим аналогично другой сигнал:

   

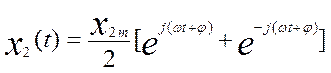
Сумма сигналов равна  сумме отклонений сигналов.

Представление входных и выходных сигналов в виде суммы двух входных сигналов и откликов позволяет полагать, что если на входе действует комплексный сигнал e^jωt, то на выходе будет сигнал e^{j(ωt+ φ)}                                                     

2.3 Преобразование Лапласа и его свойства.

                                  Пусть дана непрерывная функция f(t)

                                  Функция имеет ограничения:

                                   1. t<0=0

                                   2. Условие абсолютной сходимости

                                                     

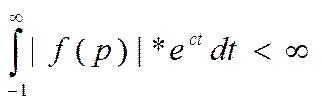
с-константа абсолютной сходимости.

Все типовые сигналы удовлетворяют данному неравенству.

Назовем функцию F(p) изображением по Лапласу от функции f(t),  если

                          F(p)=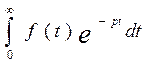   (1)

Для краткости следующую формулу записываем в виде:

F(p)=L{f(t)}  (2)          

(1), (2)- называется преобразованием Лапласа.

Для типовых сигналов f(t) изображения вычислены и сосредоточены в таблице в приложениях по ТАУ.

p-оператор преобразования сигнала

j-комплексное число

p=α+jω-который можно интерпретировать как информационный ноль пробного сигнала:

X(t)=e ^{-α t}( cos ωt+ jsin ωt)

α-показатель затухания экспоненты

ω-частота

Преобразование Лапласа ставит в соответствие  действующую функцию ¦(t) и комплекснозначное изображение:

            ¦(t)  = > F(p), которое мы будем называть изображение по Лапласу.

Преобразование Лапласа можно обратить, т.е. по изображению можно найти функцию.

            F(p)= > ¦(t)  

¦(t) – оригинал (временная функция по отображению)

Символически обратное преобразование Лапласа выглядит следующим образом:

¦(t)=L^-1{F(p)}

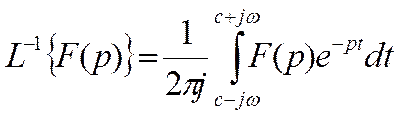
 Пример: Необходимо найти оригинал функции

¦(t)=1(t)

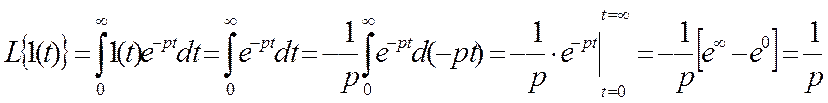
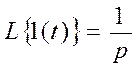
p- параметр описаний, весь спектр пробных сигналов.

Таблица прямого преобразования Фурье

Оригинал	1(t)	σ(t)	t	tn	e-αt
Изображение	1/p	1	1/p2

Оригинал	sinωt	cosωt
Изображение

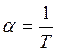
n- целое число

Свойства преобразований Лапласа

Теорема	Оригинал	Изображение
1.Линейность
2.Дифференцирование оригинала		pF(p) – ƒ(0) При начальной ординате ƒ(t)=0 дифференцирование оригинала в области изображений сводится к умножению на р, на техническом уровне р называют символом дифференцирования при переходе к изображению.
3.Интегрирование оригинала
4.Изменение масштаба по времени	ƒ(t) ƒ(tα)	F(p)
5.Смещение аргумента и оригинала	ƒ(t) ƒ(t+τ)   ƒ(t) ƒ(t-τ)   τ   τ-запаздывание	F(p)
6.Теорема о конечном значении
7.Теорема о начальном значении	ƒ(t)	F(p)

2.4Понятие передаточной функции

Передаточной функцией называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях. Если звено (система) имеет несколько входов, то при определении передаточной функции относительно какой-либо одной входной величины остальные величины полагают равными нулю.

Пусть необходимо описать звено автоматической системы, у которой имеется входной и выходной сигнал.

 

Если ограничиться случаем, когда сигнал в начальном времени, все его производные равны 0, то можно ввести величину, которая содержит всю информацию об уравнении (*) и таким образом установит связь между х и у.

Y (0)= Y’(0)=Y’’(0)=Yⁿ(0)=0

Свойства звена характеризуются передаточной функцией.

Y(p)-преобразование Лапласа от выходного сигнала X(p)-преобразование Лапласа от входного сигнала

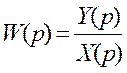
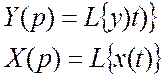
Свяжем передаточную функцию с параметрами уравнения (*). Для этого, пользуясь свойством линейности найдем изображение левой части уравнения (*).

Левая часть представляет собой сумму производных выходных сигналов с постоянным коэффициентом, следовательно передаточная функция будет суммой выходных сигналов с теми же коэффициентами.

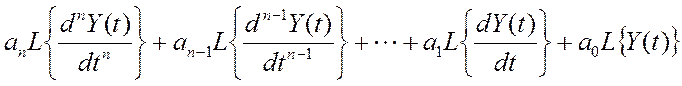
Преобразование по Лапласу правой части уравнения (*)

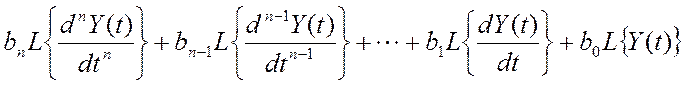
Если равны оригиналы, то должны быть равны изображения.

Приравняем левую и правую части уравнения (*) в изображениях. Это даст нам уравнение для получения передаточной функции.

Пользуясь теоремой о дифференцировании оригинала, запишем что

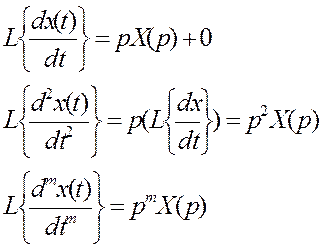
В итоге уравнение (*) принимает следующий вид в изображениях

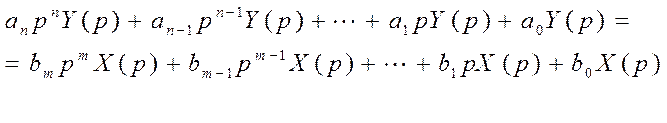
Получили алгебраическое уравнение, в котором Y(p) и X(p) можно вынести за скобку

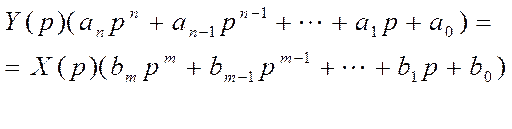
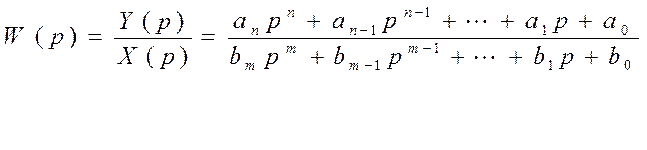
Таким образом передаточная функция линейного звена W(p) является дробно-рациональной функцией от p и содержит коэффициенты дифференциального уравнения исходно описывающего это звено:

Ограничения передаточной функции:

1.  Функция справедлива только для линейных звеньев

2.  Начальные условия на сигналы были нулевые (сами сигналы равны 0 и все их производные равны 0)