![]()
C1V – скоростная ошибка, ошибка от скорости.
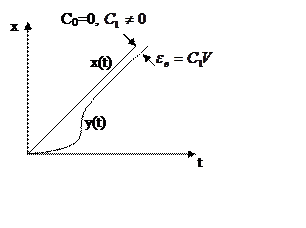 С1
– коэффициент скоростной ошибки.
С1
– коэффициент скоростной ошибки.
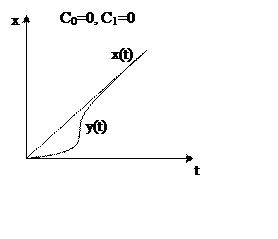 |
q=1, I
порядок астатизма Данная система называется системой
с астатизмом второго порядка и она содержит в разомкнутой системе 2 и более
интеграторов. ![]()
Определим коэффициент С1 для системы с первым порядком астатизма

KV – Добротность системы по скорости.
![]() - статический
коэффициент усиления позиционной части
- статический
коэффициент усиления позиционной части
разомкнутой системы.
Можно сказать, что общее значение
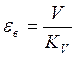
5.2.3 Режим изменения задающей величины с постоянным ускорением.
Пусть 
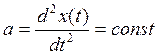 - ускорение
- ускорение
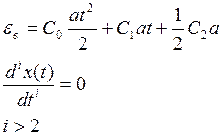
Чтобы система имела ![]() необходимо,
чтоб С0, С1=0, иначе ошибка будет неограниченно расти.
необходимо,
чтоб С0, С1=0, иначе ошибка будет неограниченно расти.
Установившееся значение ошибки ![]()
С2 – коэффициент ошибки от ускорения
Система с ошибкой от ускорения
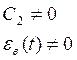
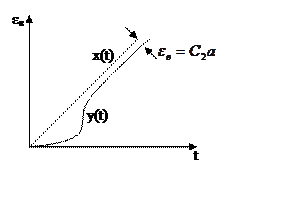 |
Система с астатизмом второго порядка (q=2), содержит в разомкнутом виде два интегрирующих звена.
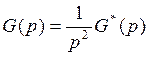
![]() - позиционная часть разомкнутой
системы.
- позиционная часть разомкнутой
системы.
Система без ошибки от ускорения
Если в системе С2=0, εв=0, то это система без ошибки от ускорения.
 |
Система с астатизмом выше второго порядка
q>2
Свяжем С2 с передаточной функцией разомкнутой системы
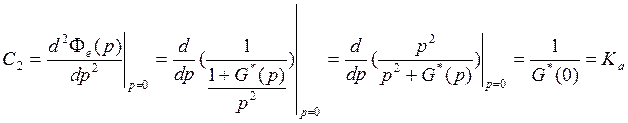
![]() - коэффициент
усиления позиционной части разомкнутой системы, добротность системы по
ускорению.
- коэффициент
усиления позиционной части разомкнутой системы, добротность системы по
ускорению.
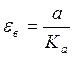
5.2.4 Связь астатизма системы с ЛАЧХ разомкнутой системы.
Порядок астатизма – целое число q, которое равно
порядку в описании входного сигнала ![]() , при котором
установившаяся ошибка постоянна и отлична от нуля.
, при котором
установившаяся ошибка постоянна и отлична от нуля.
![]()
 1.
1.


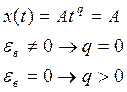
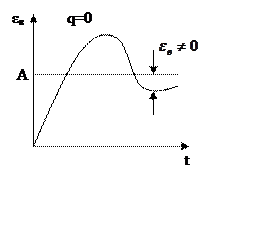 |
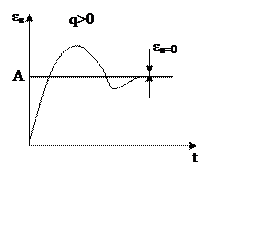 |
||
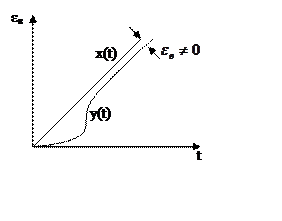
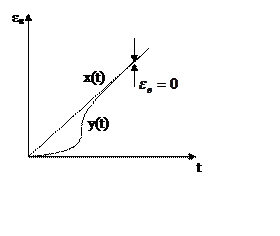 2.
2. ![]()
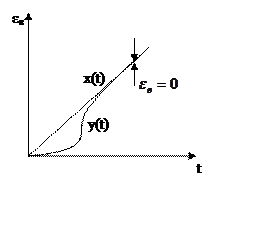 3.
3. ![]()
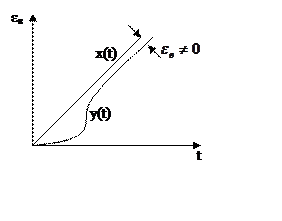 |
q=2 q>2
На практике астатизм выше второго порядка (q>2) не применяется, поэтому мы их не рассматриваем.
5.2.5 Способы определения порядка астатизма
1. По коэффициентам ошибок
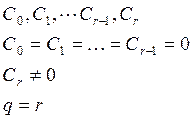
2. По количеству интегрирующих звеньев в передаточной функции разомкнутой системы.
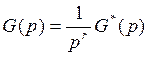 - позиционная
часть системы
- позиционная
часть системы
Система имеет r интеграторов и q=r
3.По наклону ЛАЧХ в низкочастотной области.
Предположим, что передаточная функция разомкнутой системы имеет вид
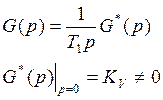
 Тогда
ЛАЧХ будет иметь следующий вид.
Тогда
ЛАЧХ будет иметь следующий вид.
Пусть 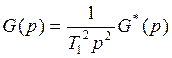 , где
, где
![]() - позиционная
часть
- позиционная
часть
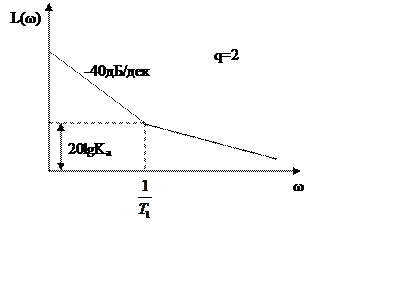 |
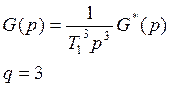
Этот случай в жизни практически не встречается
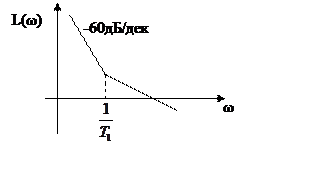
В итоге, астатизм системы определяется по ЛАЧХ следующим образом
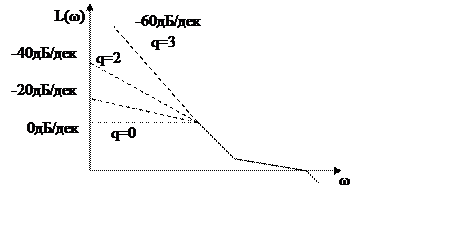 |
5.2.6 Исследование точности в условиях действия управляющих и возмущающих сигналов
В общем случае на систему действуют как управляющие (задающие), так и возмущающие сигналы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.