Рациональность СВП-С в относительно мелководных районах. Выбор главных размерений, страница 20

Определение эйлеровых напряжений пластин обшивки судна и оценка устойчивости продольных ребер жесткости.

Пластины считаются свободно опертыми на опорном контуре.

Эйлеровы напряжения пластин обшивки судна

Таблица 9

Критические напряжения продольных ребер жесткости

Таблица 10

Наименование ребра жесткости	профиль	Размеры присоед. пояска(мм)		Пролет l (см)	Площадь поперечного сечения F (см²)	Момент инерции площади поперечного сечения I(см⁴)	Теоретические эйлеровы напряжения σ=π²ЕY/l²F	Предел текучести материала σ_т(кг/см²)	σ_э/ σ_т	критич. напряж σ_пр(кг/см²)
Наименование ребра жесткости	профиль	при вычислении мом-та инерции	при вычислении S поперечн. сечения	Пролет l (см)	Площадь поперечного сечения F (см²)	Момент инерции площади поперечного сечения I(см⁴)	Теоретические эйлеровы напряжения σ=π²ЕY/l²F	Предел текучести материала σ_т(кг/см²)	σ_э/ σ_т	критич. напряж σ_пр(кг/см²)
1	2	3	4	5	6	7	8	9	10	11
ребра жесткости скега	6	4х160	4x400	100	19.2	48.1	170	1800	0.094	1600
ребра жесткости скега	6	3x120	3x300	100	12.2	36.9	210	1600	0.130	1390
ребра жесткости борта	6	3x120	3x350	100	13.7	36.9	185	1600	0.115	1360
ребра жесткости тента	┌┘ 40x25x1.5x2	1.5x60	1.5x200	100	4.6	11.2	170	1600	0.105	1000

Оценка устойчивости перекрытия тента

Перекрытие тента состоит (в районе салона) из листов S=2 мм и профилей ┌┘40х25х1,5х2

Элементы перекрытия

Длинна l=17 м

Ширина α=7 м расстояние между бимсами а=1 м расстояние между ребрами жесткости b=0.2 м карлингсами b₁=1.3 м

Момент инерции и площадь поперечного сечения ребра с присоедниенным пояском

i=11.2 f=4.6

Элементы сечения карлингса

i₁=252 см⁴

f₁=7 см²

Необходимый момент инерции бимса

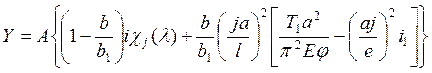
Где Т₁=σ_прf₁ – усилие действующее на корпус

σ_кр – заданное критическое напряжение

j – число полуволн потери устойчивости

А=(π/μ)⁴(L/a)³Lφ/b=0.595*(6/1)³*6*1/0.2=380

(π/μ)⁴=0.595 – коэффициент определяющийся в зависимости от коэффициента опорной пары бимсов (æ=0,5) и отношения l₁/α=0

l₁=0 ширина перекрытия не одкрепленная продольными балками

φ=1 – коэффициент учитывающий влияние отступления от закона Гука

χ_j(λ) – функция параметра λ =σ_кр/σ_эφ и числа j

σ_э=1000

σ_э<0.5σ_т=1050 (кг/см²)

I=kI₀ , где I₀=А_iχ_j(λ) – необходимый момент инерции бимса без учета влияния карлингсов

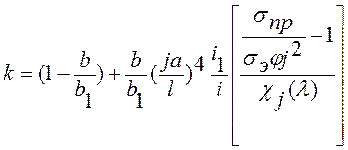- коэффициент учитывающий влияние карлингсов

Е=0,7*106

σ_э=π²Ei₁/l²f₁=9.85*0.7*10⁶*252/17*17*7*10⁴=86 кг/см²

Эйлеровы напряжения в карлингсах пролета l=17 м

В рассматриваемом случае наибольшее значение необходимого момента инерции бимса имеет место при j =1

Зависимость I=f(σ_кр)

Таблица 11