Часть II
Мера, интеграл Лебега,
гильбертово пространство
Понятие меры ![]() множества А является естественным
обобщением понятий:
множества А является естественным
обобщением понятий:
1) длины ![]() отрезка
отрезка
![]()
2) площади S(F) плоской фигуры F,
3) объема V(G) пространственной фигуры G,
4) приращения ![]() неубывающей функции
неубывающей функции ![]() на полуинтервале [а, b),
на полуинтервале [а, b),
5) интеграла от неотрицательной функции, взятого по некоторой линейной, плоской или пространственной области, и т. п.
Понятие меры множества, возникшее первоначально в теории функций действительного переменного, нашло в дальнейшем многочисленные применения в теории вероятностей, теории динамических систем, функциональном анализе и других областях математики.
В первом параграфе этой главы мы изложим понятие меры для множеств на плоскости, отправляясь от понятия площади прямоугольника. Общая теория меры будет изложена в § 35-39. Читатель легко заметит, однако, что все рассуждения, проведенные в §33, имеют общий характер и в абстрактной теории повторяются без существенных изменений.
Рассмотрим систему ![]() множеств на плоскости (х,у), каждое
из которых определяется одним из неравенств вида
множеств на плоскости (х,у), каждое
из которых определяется одним из неравенств вида
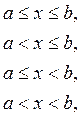
и одним из неравенств вида
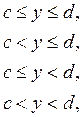
где а, b, с, и d — произвольные числа. Множества, принадлежащие этой системе, мы будем называть «прямоугольниками». Замкнутый прямоугольник, определяемый неравенствами
![]()
представляет собой прямоугольник в обычном
смысле (вместе с границей), если ![]() и
и ![]() или отрезок (если
или отрезок (если ![]() и
и
![]() или
или ![]() и
и ![]() ), или точку (при
), или точку (при ![]() ),или, наконец, пустое множество (если а > b или с > d). Открытый «прямоугольник»
),или, наконец, пустое множество (если а > b или с > d). Открытый «прямоугольник»
![]()
представляет собой, в зависимости от соотношений между а, b, с и d, прямоугольник без границ или пустое множество. Каждый из прямоугольников остальных типов (назовем их полуоткрытыми) представляет собой либо настоящий прямоугольник без одной, двух или трех сторон, либо интервал, либо полуинтервал, либо, наконец, пустое множество.
Для каждого из прямоугольников определим его меру, в соответствии с известным из элементарной геометрии понятием площади, следующим образом:
а) мера пустого множества равна нулю;
б) мера непустого прямоугольника (замкнутого, открытого или полуоткрытого), определяемого числами а, b, с и d, равна
![]()
Таким образом, каждому прямоугольнику Р поставлено в соответствие число т(Р) — мера этого прямоугольника; при этом выполнены, очевидно, следующие условия:
1) Мера т(Р) принимает действительные неотрицательные значения;
2) Мера m(Р)
аддитивна, т. е. если 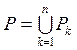 и
и ![]() при
при ![]() то
то
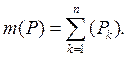
Нашей задачей является распространение, с сохранением свойств 1) и 2), меры т(Р), определенной пока лишь для прямоугольников, на более широкий класс множеств.
Первый шаг в этом направлении состоит в распространении понятия меры на так называемые элементарные множества. Назовем плоское множество элементарным, если его можно представить, хотя бы одним способом, как соединение конечного числа попарно непересекающихся прямоугольников.
Для дальнейшего нам понадобится следующая
Теорема 1. Соединение, пересечение, разность и симметрическая разность двух элементарных множеств также являются элементарными множествами.
Доказательство. Ясно, что пересечение двух прямоугольников есть снова прямоугольник. Поэтому, если
![]()
— два элементарных множества, то и
![]()
также является элементарным множеством.
Разность двух прямоугольников есть, как легко проверить, элементарное множество. Следовательно, вычитая из прямоугольника некоторое элементарное множество, мы снова получим элементарное множество (как пересечение элементарных). Пусть теперь A и В — два элементарных множества. Найдется, очевидно, прямоугольник Р, содержащий каждое из них. Тогда
![]()
есть элементарное множество, в силу сказанного выше. Отсюда и из равенств
![]()
и
![]()
следует, что разность и симметрическая разность элементарных множеств являются элементарными множествами. Теорема доказана.
Определим теперь меру ![]() для элементарных множеств следующим
образом: если
для элементарных множеств следующим
образом: если
![]()
где ![]() — попарно не
пересекающиеся прямоугольники, то
— попарно не
пересекающиеся прямоугольники, то
![]()
Покажем, что ![]() не
зависит от способа представления множества А в виде суммы прямоугольников.
Пусть
не
зависит от способа представления множества А в виде суммы прямоугольников.
Пусть
![]()
где ![]() и
и ![]() —
прямоугольники, и
—
прямоугольники, и ![]() при
при ![]() Так как
пересечение
Так как
пересечение ![]() двух прямоугольников есть прямоугольник,
то, в силу аддитивности меры для прямоугольников,
двух прямоугольников есть прямоугольник,
то, в силу аддитивности меры для прямоугольников,
![]()
Легко видеть, что мера элементарных множеств, определенная таким образом, неотрицательна и аддитивна.
Установим следующее важное для дальнейшего свойство меры элементарных множеств.
Теорема 2. Если А — элементарное
множество и ![]() — конечная или счетная система
элементарных множеств, такая, что
— конечная или счетная система
элементарных множеств, такая, что
![]()
то
![]() (1)
(1)
Доказательство. Для любого ![]() и данного А можно, очевидно, найти
такое замкнутое элементарное множество
и данного А можно, очевидно, найти
такое замкнутое элементарное множество ![]() которое
содержится в А и удовлетворяет условию:
которое
содержится в А и удовлетворяет условию:
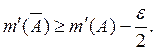
(Для этого достаточно каждый из k составляющих А прямоугольников ![]() заменить целиком лежащим в нем
замкнутым прямоугольником с площадью большей, чем
заменить целиком лежащим в нем
замкнутым прямоугольником с площадью большей, чем 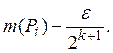 )
)
Далее, для каждого ![]() можно найти открытое элементарное
множество
можно найти открытое элементарное
множество ![]() содержащее
содержащее ![]() и
удовлетворяющее условию
и
удовлетворяющее условию
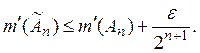
Ясно, что
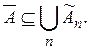
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.