Мера, интеграл Лебега, гильбертово пространство, страница 12

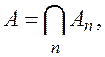
то

а если  — возрастающая цепочка измеримых множеств и

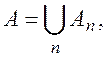
то

Доказательство, приведенное в § 33 для плоской меры (теорема 10), дословно переносится на общий случай.

1.  Из результатов §37 и 38 легко заключить, что каждое множество А, измеримое по Жордану, измеримо и по Лебегу, причем его жорданова и лебегова меры одинаковы. Отсюда непосредственно вытекает, что жорданово продолжение - аддитивной меры  - аддитивно.

2. Каждое множество А, измеримое по Лебегу, является множеством однозначности для исходной меры т. Действительно, при любом  для А существует такое что. Каково бы ни было определенное для А продолжение  меры т,

так как продолжение меры m на  однозначно. Далее,

и, следовательно,

Таким образом, для любых двух продолжений и  меры m имеем:

откуда, в силу произвольности ,

Можно показать, что система множеств, измеримых по Лебегу, исчерпывает всю систему множеств однозначности для исходной меры m.

3. Пусть m - некоторая - аддитивная мера с областью определения S и M  — область определения ее лебеговского продолжения. Из теоремы 3 этого параграфа легко следует, что каково бы ни было полукольцо , такое, что

 M, всегда

§ 39. Продолжение мер по Лебегу в общем случае

Если полукольцо , на котором определена исходная мера m, не имеет единицы, то изложение § 38 должно быть несколько изменено. Определение 12 верхней меры сохраняется, но верхняя мера  оказывается определенной только на системе  таких множеств А, для которых существует покрытие множествами из с конечной суммой

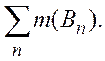
Определение 13 теряет смысл. Нижняя мера может быть определена (несколько иным способом) и в общем случае, но мы не будем этим заниматься. За определение измеримости множества целесообразно взять теперь свойство измеримых множеств, указываемое теоремой 3.

Определение 1. Множество А называется измеримым, если при любом  существует множество такое, что

Теоремы 4, 5, 6 и заключительное определение 4 сохраняет силу. В доказательствах предположение о существовании единицы использовалось лишь в доказательстве теоремы 4. Чтобы дать доказательство теоремы 4 в общем случае, надо доказать заново, что из вытекает Доказательство это проводится точно так же, как и для на основе включения

В случае, когда не имеет единицы, теорема 7 § 38, заменяется следующей теоремой.

Теорема 1. При любой исходной мере т система множествM, измеримых по Лебегу, является - кольцом, измеримость же множества 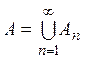 при измеримых  имеет место в том и только в том случае, если меры 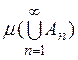 ограничены некоторой константой, не зависящей от N.

Доказательство этого утверждения предоставляется читателю.

Замечание. В нашем изложении меры всегда конечны, так что необходимость последнего условия очевидна.

Из теоремы 1 вытекает такое

Следствие. Система M всех множеств M, являющихся подмножествами фиксированного множества M, образует борелевскую алгебру. Например, система всех измеримых по Лебегу (в смысле обычной лебеговой меры на прямой) подмножеств любого отрезка [а, b] есть борелевская алгебра множеств.

В заключение отметим еще одно свойство лебеговых мер.

Определение 2. Мера называется полной, если из  и вытекает

Очевидно, что при этом . Без всякого труда доказывается, что лебегово продолжение любой меры полно. Это вытекает из того, что при  и  неизбежно , а любое множество С, для которого , измеримо, так как , и

Укажем на связь между процессом продолжения меры по Лебегу и процессом пополнения метрического пространства. Заметим для этого, что можно принять за расстояние между элементами А, В кольца . Тогда  становится метрическим (вообще говоря, неполным) пространством, и его пополнение, согласно теореме 3 § 38, состоит как раз из всех измеримых множеств. (При этом, однако, с метрической точки зрения, множества А и B неразличимы, если )