то при любом ![]() существуют А' и А"
из
существуют А' и А"
из ![]() такие, что
такие, что
![]()
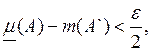
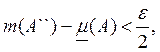
![]()
т.е.
![]()
Для множеств из M имеют место следующие теоремы.
Теорема 3. Если 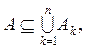 то
то ![]()
Доказательство. Выберем такие ![]() , что
, что
![]()
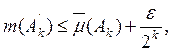
и образуем 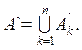 Тогда
Тогда
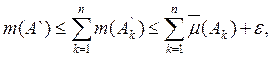
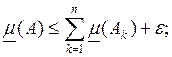
так как ![]() произвольно, то
произвольно, то 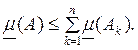
Теорема 4. Если ![]() и
и ![]() то
то
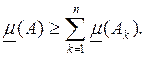
Доказательство. Выберем ![]() такие, что
такие, что 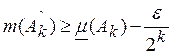 и образуем
и образуем 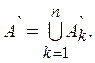 Тогда
Тогда
![]() и
и 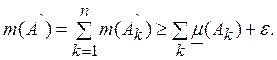 Так
как
Так
как ![]() то
то 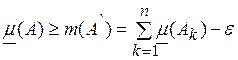 Поскольку
Поскольку
![]() произвольно,
произвольно, 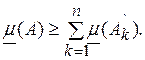
Определим теперь функцию ![]() с областью определения
с областью определения
![]()
как общее значение внешней и внутренней меры:
![]()
Из теорем 3 и 4 и из того очевидного обстоятельства, что
для ![]()
![]()
вытекает
Теорема 5. Функция ![]() является мерой и
продолжением меры т.
является мерой и
продолжением меры т.
Доказательство. Изложенное
построение применимо к любой мере ![]() , определенной на
кольце.
, определенной на
кольце.
Система
![]() элементарных множеств плоскости
существенно связана с системой координат: множества системы
элементарных множеств плоскости
существенно связана с системой координат: множества системы ![]() составляются из прямоугольников со
сторонами, параллельными осям координат. При переходе к мере Жордана
составляются из прямоугольников со
сторонами, параллельными осям координат. При переходе к мере Жордана
![]()
эта зависимость от выбора системы координат исчезает:
отправляясь от любой системы координат ![]() связанной
с первоначальной системой
связанной
с первоначальной системой ![]() ортогональным преобразованием
ортогональным преобразованием
![]()
![]()
мы получим одну и ту же меру Жордана
![]()
(здесь ![]() означает меру,
построенную при помощи прямоугольников со сторонами, параллельными осям
означает меру,
построенную при помощи прямоугольников со сторонами, параллельными осям ![]() и
и ![]() ). Этот
факт может быть обоснован при помощи такой общей теоремы:
). Этот
факт может быть обоснован при помощи такой общей теоремы:
Теорема 6. Для того чтобы жордановы продолжения ![]() и
и ![]() мер
мер ![]() и
и ![]() определенных
на кольцах
определенных
на кольцах ![]() и
и ![]() ,
совпадали, необходимо и достаточно выполнение условий:
,
совпадали, необходимо и достаточно выполнение условий:
![]()
![]() на
на ![]()
![]()
![]() на
на ![]()
Необходимость условий очевидна. Докажем их достаточность.
Пусть ![]() Тогда
существуют такие
Тогда
существуют такие ![]()
![]() что
что ![]()
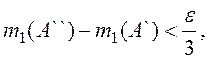 и
и ![]() По условию
теоремы,
По условию
теоремы, ![]() и
и ![]()
Из определения меры ![]() следует,
что существуют
следует,
что существуют ![]() и
и ![]() для
которых
для
которых
![]() и
и 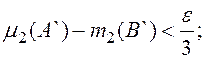
![]() и
и 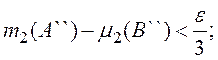
при этом
![]()
и, очевидно,
![]()
Так как ![]() произвольно, то
произвольно, то ![]() а из соотношений
а из соотношений
![]()
вытекает, что
![]()
Теорема доказана.
Теперь для установления независимости меры Жордана на плоскости от выбора системы координат остается лишь убедиться в том, что множество, получающееся из элементарного поворотом на некоторый угол а, измеримо по Жордану. Читателю предлагается проделать это самостоятельно.
Если исходная мера га определена не на кольце, а на полукольце, то ее жордановым продолжением естественно назвать меру
![]()
получающуюся в результате продолжения ![]() на кольцо
на кольцо ![]() и
дальнейшего продолжения по Жордану.
и
дальнейшего продолжения по Жордану.
Часто приходится рассматривать соединения не только конечного, но и счетного числа множеств. В связи с этим условие аддитивности, которое мы наложили на меры (определение 1 § 34), оказывается недостаточным и его естественно заменить более сильным требованием счетной аддитивности.
Определение 1. Мера ![]() называется счетно-аддитивной
(или
называется счетно-аддитивной
(или ![]() - аддитивной) , если для любых
множеств
- аддитивной) , если для любых
множеств ![]() принадлежащих ее области определения
принадлежащих ее области определения ![]() и удовлетворяющих условиям
и удовлетворяющих условиям
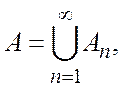
![]() при
при ![]()
имеет место равенство
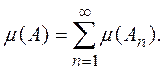
Плоская мера Лебега, построенная нами в § 33, ![]() -аддитивна (теорема 9). Пример
-аддитивна (теорема 9). Пример ![]() -аддитивной меры совсем иной природы можно
построить следующим образом. Пусть
-аддитивной меры совсем иной природы можно
построить следующим образом. Пусть
![]()
— произвольное счетное множество и числа ![]() таковы, что
таковы, что
![]()
Область ![]() состоит из всех
подмножеств множества X. Для каждого
состоит из всех
подмножеств множества X. Для каждого ![]() положим
положим
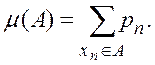
Легко проверить, что ![]() будет
будет
![]() - аддитивной мерой, причем
- аддитивной мерой, причем ![]() Этот пример естественно появляется в связи
со многими вопросами теории вероятностей.
Этот пример естественно появляется в связи
со многими вопросами теории вероятностей.
Укажем пример меры аддитивной,
но не ![]() - аддитивной. Пусть X — множество всех рациональных точек отрезка [0,1], а
- аддитивной. Пусть X — множество всех рациональных точек отрезка [0,1], а ![]() состоит из пересечений множества X с произвольными интервалами (a, b),
сегментами [а, b] или полусегментами [а, b), (а, b]. Легко
видеть, что
состоит из пересечений множества X с произвольными интервалами (a, b),
сегментами [а, b] или полусегментами [а, b), (а, b]. Легко
видеть, что ![]() представляет собой полукольцо. Для каждого
такого множества положим
представляет собой полукольцо. Для каждого
такого множества положим
![]()
Это аддитивная мера. Она не будет ![]() -аддитивна,
так как, например,
-аддитивна,
так как, например, ![]() и в то же время X есть сумма счетного числа отдельных точек, каждая из
которых имеет меру нуль.
и в то же время X есть сумма счетного числа отдельных точек, каждая из
которых имеет меру нуль.
В этом и двух следующих параграфах мы будем
рассматривать ![]() - аддитивные меры и различные их
- аддитивные меры и различные их ![]() - аддитивные продолжения.
- аддитивные продолжения.
Теорема 1. Если мера ![]() , определенная на
некотором полукольце
, определенная на
некотором полукольце ![]() , счетно-аддитивна, то и мера
, счетно-аддитивна, то и мера ![]() получающаяся ее продолжением на кольцо
получающаяся ее продолжением на кольцо ![]() счетно-аддитивна.
счетно-аддитивна.
Доказательство. Пусть
![]()
![]() n = 1, 2, … , и
n = 1, 2, … , и
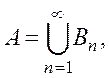
причем ![]() при
при ![]() . Тогда существуют такие множества
. Тогда существуют такие множества ![]() и
и ![]() из
из
![]() что
что
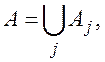
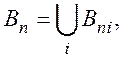
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.